
分析 連接OB、OC,作OD⊥BC于D,則∠ODB=90°,由垂徑定理得出BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$cm,由等腰三角形的性質(zhì)得出∠BOD=∠COD=$\frac{1}{2}$∠BOC,由三角函數(shù)求出∠BOD=60°,得出∠BOC=120°,由圓周角定理即可得出結(jié)果.
解答 解:分兩種情況: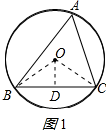
①當(dāng)△ABC是銳角三角形時(shí);連接OB、OC,作OD⊥BC于D,如圖1所示:
則∠ODB=90°,BD=CD=$\frac{1}{2}$BC=$\sqrt{3}$cm,∠BOD=∠COD=$\frac{1}{2}$∠BOC,
∵sin∠BOD=$\frac{BD}{OB}$,
∴∠BOD=60°,
∴∠BOC=120°,
∴∠A=$\frac{1}{2}$∠BOC=60°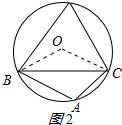
②當(dāng)△ABC是鈍角三角形時(shí),如圖2所示:
∠A=180°-60°=120°;
綜上所述:∠A的度數(shù)為60°或120°,
故答案為:60或120.
點(diǎn)評(píng) 本題考查了三角形的外接圓、垂徑定理、等腰三角形的性質(zhì)、圓周角定理、三角函數(shù)等知識(shí);本題綜合性強(qiáng),難度適中.


 沖刺100分單元優(yōu)化練考卷系列答案
沖刺100分單元優(yōu)化練考卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
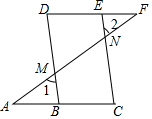 補(bǔ)全證明過程,即在橫線處填上遺漏的結(jié)論或理由.
補(bǔ)全證明過程,即在橫線處填上遺漏的結(jié)論或理由.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知點(diǎn)B,C,F(xiàn),E在同一直線上,AB=DE,BC=EF,AB∥DE.求證:AC∥DF.
如圖,已知點(diǎn)B,C,F(xiàn),E在同一直線上,AB=DE,BC=EF,AB∥DE.求證:AC∥DF.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知:∠B=∠C=90°,M是BC的中點(diǎn),DM平分∠ADC.
如圖,已知:∠B=∠C=90°,M是BC的中點(diǎn),DM平分∠ADC.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com