【題目】點A、B在數軸上的位置如圖所示：
（1）點A表示的數是 ，點B表示的數是 ；
（2）在原圖中分別標出表示+1.5的點C、表示﹣3.5的點D；
（3）在上述條件下，B、C兩點間的距離是 ，A、C兩點間的距離是 ．
口算心算速算應用題系列答案
同步拓展閱讀系列答案科目：初中數學 來源： 題型：
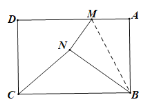
【題目】如圖，矩形紙片ABCD中，AD＝5，AB＝3．若M為射線AD上的一個動點，將△ABM沿BM折疊得到△NBM．若△NBC是直角三角形．則所有符合條件的M點所對應的AM長度的和為______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y＝ax2＋bx＋c（a≠0）的圖象如圖所示，有下列5個結論： ① c=0；②該拋物線的對稱軸是直線x=﹣1；③當x=1時，y=2a；④am
+bm+a＞0（m≠﹣1）；⑤設A（100，y），B（﹣100，y
）在該拋物線上，則y＞y
．其中正確的結論有___________ ．（寫出所有正確結論的序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學活動：擦出智慧的火花---------由特殊到一般的數學思想．
數學課上，李老師出示了問題：如圖1，四邊形ABCD是正方形，點E是邊BC上的點，過點E作EF⊥AE,過點F作FG⊥BC交BC的延長線于點G..
（1）求證：∠BAE=∠FEG.
（2）同學們很快做出了解答，之后李老師將題目修改成：如圖2，四邊形ABCD是正方形，點E是邊BC的中點．∠AEF=90°，且EF交正方形外角∠DCG的平分線于點F，求證：AE=EF．
經過思考，小明展示了一種正確的解題思路：取AB的中點M，連接ME，則AM=EC，易證△AME≌△ECF，所以AE＝EF．請借助圖1完成小明的證明；
在（2）的基礎上，同學們作了進一步的研究：
（3）小聰提出：如圖2，如果把“點E是邊BC的中點”改為“點E是邊BC上（除B，C外）的任意一點”，其它條件不變，那么結論“AE=EF”仍然成立，你認為小聰的觀點正確嗎？如果正確，寫出證明過程；如果不正確，請說明理由；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，BI，CI分別平分∠ABC，∠ACB，過I點作DE∥BC，交AB于D，交AC于E，給出下列結論：①△DBI是等腰三角形；②△ACI是等腰三角形；③AI平分∠BAC；④△ADE周長等于AB＋AC.其中正確的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖，兩個圈分別表示負數集和分數集. 請你把下列各數填入表示它所在的數集的圈里：
-50% ， 2011 ， 0.618 ， -3 ，
，0 ， 5.9，-3.14 ， -92 .
（2）圖中，這兩個圈的重疊部分表示什么數的集合？
（3）在（1）的數據中，求最大的數與最小的數之和.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在面積為60的平行四邊形ABCD中，過點A作AE垂直于直線BC于點E，作AF垂直于直線CD于點F，若AB=10，BC=12，則CE+CF的值為（ ）
A. 22-11
B. 
C. 或
D. 
或
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD中，AB=6，BC=4，過對角線BD中點O的直線分別交AB，CD邊于點E，F．
（1）求證：四邊形BEDF是平行四邊形；
（2）當四邊形BEDF是菱形時，求EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知兩點
、
在數軸上，
，點表示的數是
，且與
互為相反數．
（1）寫出點表示的數；
（2）如圖1，當點、位于原點
的同側時，動點
、
分別從點、處在數軸上同時相向而行，動點的速度是動點的速度的2倍，3秒后兩動點相遇，當動點到達點4時，運動停止．在整個運動過程中，當
時，求點、所表示的數；
（3）如圖2，當點、位于原點的異側時，動點、分別從點、處在數軸上向右運動，動點比動點晚出發1秒；當動點運動2秒后，動點到達點
處，此時動點立即掉頭以原速向左運動3秒恰與動點相遇；相遇后動點又立即掉頭以原速向右運動5秒，此時動點到達點
處，動點到達點
處,當
時，求動點、運動的速度．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
