
分析 求出二次函數(shù)對稱軸為直線x=m,再分m≤1,m>兩種情況,根據(jù)二次函數(shù)的增減性列方程求解即可.
解答 解:二次函數(shù)對稱軸為直線x=m,
①m≤1時,x=m取得最大值,m2+1=4,
解得m=±$\sqrt{3}$,
∵m=$\sqrt{3}$都不滿足-1≤m≤1的范圍,
∴m=-$\sqrt{3}$;
②m>1時,x=1取得最大值,-(1-m)2+m2+1=4,
解得m=2.
綜上所述,m=-$\sqrt{3}$或2時,二次函數(shù)有最大值4.
故答案為:2或$-\sqrt{3}$.
點評 本題考查了二次函數(shù)的最值,熟悉二次函數(shù)的性質(zhì)及圖象是解題的關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:填空題
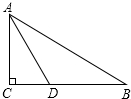 如圖,在△ABC中,∠C=90°,AD平分∠CAB,BC=10cm,BD=5cm,那么D點到直線AB的距離是5cm.
如圖,在△ABC中,∠C=90°,AD平分∠CAB,BC=10cm,BD=5cm,那么D點到直線AB的距離是5cm.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 在數(shù)學(xué)活動課上,老師帶領(lǐng)學(xué)生去測量操場上樹立的旗桿的高度,老師為同學(xué)們準(zhǔn)備了如下工具:①高為m米的測角儀,②長為n米的竹竿,③足夠長的皮尺.請你選用以上的工具,設(shè)計一個可以通過測量,求出國旗桿高度的方案(不用計算和說明,畫出圖形并標(biāo)記可以測量的長度或者角度即可,可測量的角度選用α,β,γ標(biāo)記,可測量的長度選用a,b,c,d標(biāo)記,測角儀和竹竿可以用線段表示).
在數(shù)學(xué)活動課上,老師帶領(lǐng)學(xué)生去測量操場上樹立的旗桿的高度,老師為同學(xué)們準(zhǔn)備了如下工具:①高為m米的測角儀,②長為n米的竹竿,③足夠長的皮尺.請你選用以上的工具,設(shè)計一個可以通過測量,求出國旗桿高度的方案(不用計算和說明,畫出圖形并標(biāo)記可以測量的長度或者角度即可,可測量的角度選用α,β,γ標(biāo)記,可測量的長度選用a,b,c,d標(biāo)記,測角儀和竹竿可以用線段表示).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=2(1+x%) | C. | 12%+7%=2x% | D. | (1+12%)(1+7%)=(1+x%)2 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com