
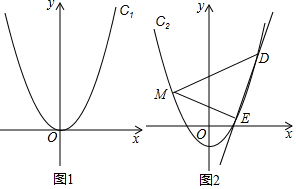
分析 (1)把點的坐標代入拋物線解析式可求得a的值,則可求得拋物線解析式,可求得其頂點坐標和對稱軸;
(2)由直線l解析式可求得P點坐標,設A(x1,y1)、B(x2,y2),由PA=AB和聯(lián)立直線和拋物線解析式,可求得A的坐標;
(3)過點M作直線l∥x軸,過點D作DF⊥l于F,過點E作EG⊥l于G,設D(x1,x12-h)、E(x2,x22-h),由相似三角形的性質可求得x1+x2=4,設直線DE解析式為y=kx+b,把D、E坐標代入可求得k=x1+x2=4,可證得結論.
解答 解:
(1)∵拋物線C1:y=ax2經過(-1,1),
∴a=1,
∴拋物線解析式為y=x2,
∴頂點坐標為(0,0),對稱軸為y軸,
故答案為:y=x2;(0,0);對稱軸為y軸;
(2)∵當x=-2時,y=-2,
∴P(-2,-2),
設A(x1,y1)、B(x2,y2)
∵PA=PB
∴-2+x2=2x1①
聯(lián)立$\left\{\begin{array}{l}y=kx+2k-2\\ y={x^2}\end{array}\right.$,整理得x2-kx-2k+2=0
∴x1+x2=k ②,x1x2=-2k+2 ③
由①得,${x_1}=\frac{k-2}{3}$,代入②③得,$k=-4±3\sqrt{3}$,
∴A點坐標為($\sqrt{3}-2$,$7-4\sqrt{3}$)或($-\sqrt{3}-2$,$7+4\sqrt{3}$);
(3)過點M作直線l∥x軸,過點D作DF⊥l于F,過點E作EG⊥l于G,
設D(x1,x12-h)、E(x2,x22-h),則△MDF∽△MEG,
∴$\frac{{({x_1}^2-h)-(4-h)}}{{{x_1}+2}}=\frac{{-[({x_2}^2-h)-(4-h)]}}{{{x_2}+2}}$,得x1+x2=4,
設直線DE的解析式為y=kx+b
∴$\left\{\begin{array}{l}k{x_1}+b={x_1}^2-h\\ k{x_2}+b={x_2}^2-h\end{array}\right.$,得k=x1+x2=4
∴直線DE一定與過原點的直線y=4x平行.
點評 本題為二次函數的綜合應用,涉及待定系數法、函數圖象的交點、一元二次方程根與系數的關系、兩直線平行、相似三角形的性質等知識.在(1)中注意待定系數法的應用步驟,在(2)中根據函數圖象的交點整理得到x1、x2和k的關系是解題的關鍵,在(3)用D、E的坐標表示出k是解題的關鍵.本題考查知識點較多,綜合性較強,難度較大.


 優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案
優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數學 來源: 題型:填空題
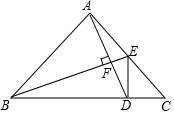 如圖,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB,D、E分別是BC、AC上的點,若AD⊥BE,∠ADB=∠CDE,CE=2,則S△ADE=$\frac{4}{3}$.
如圖,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB,D、E分別是BC、AC上的點,若AD⊥BE,∠ADB=∠CDE,CE=2,則S△ADE=$\frac{4}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{13}$ | D. | $\frac{1}{52}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
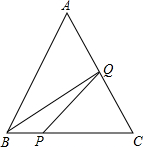 在△ABC中,已知AB=BC=CA=4cm,點P、Q分別從B、C兩點同時出發(fā),其中點P沿BC向終點C運動,速度為1cm/s;點Q沿CA、AB向終點B運動,速度為2cm/s,設它們運動的時間為x(s),當x=2或$\frac{16}{5}$,△BPQ是直角三角形.
在△ABC中,已知AB=BC=CA=4cm,點P、Q分別從B、C兩點同時出發(fā),其中點P沿BC向終點C運動,速度為1cm/s;點Q沿CA、AB向終點B運動,速度為2cm/s,設它們運動的時間為x(s),當x=2或$\frac{16}{5}$,△BPQ是直角三角形.查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com