
【題目】如圖,在 ![]() 中,
中,![]() ,
,![]() ,
,![]() 的垂直平分線交
的垂直平分線交 ![]() 于點
于點 ![]() ,交
,交 ![]() 于點
于點 ![]() ,連接
,連接 ![]() .
.

(1)求 ![]() 的周長;
的周長;
(2)若 ![]() ,求
,求 ![]() 的度數(shù).
的度數(shù).
【答案】(1)27;(2)75°
【解析】
(1)根據(jù)線段垂直平分線的性質(zhì)易得到△ABD的周長=AB+BC;
(2)根據(jù)等腰三角形的的性質(zhì)得到∠C=∠B=∠CAD=35°,然后由三角形內(nèi)角和定理即可求∠BAD的度數(shù).
解:(1)∵DE是AC的垂直平分線,
∴AD=CD,
∵AB=AC=12,BC=15,
∴△ABD的周長是:AB+BD+AD=AB+BD+CD=AB+BC=12+15=27;
(2)∵AB=AC,∠B=35°,
∴∠B=∠C=35°,.
又∵DE是AC的垂直平分線,
∴AD=CD,
∴∠DAC=∠C=35°,
∴∠BAD=180°∠B∠C∠DAC=180°105°=75°.
故答案為:(1)27;(2)75°


 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案 單元加期末復(fù)習(xí)先鋒大考卷系列答案
單元加期末復(fù)習(xí)先鋒大考卷系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,平面直角坐標(biāo)系![]() 中
中![]() ,
,![]() ,
,![]() .
.

(1)作出![]() 關(guān)于直線
關(guān)于直線![]() 對稱的圖形△
對稱的圖形△![]() 并寫出△
并寫出△![]() 各頂點的坐標(biāo);
各頂點的坐標(biāo);
(2)將△![]() 向左平移2個單位,作出平移后的△
向左平移2個單位,作出平移后的△![]() ,并寫出△
,并寫出△![]() 各頂點的坐標(biāo);
各頂點的坐標(biāo);
(3)觀察![]() 和△
和△![]() ,它們是否關(guān)于某直線對稱?若是,請指出對稱軸,并求
,它們是否關(guān)于某直線對稱?若是,請指出對稱軸,并求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ABC=∠ADC=45°,將△BCD繞點C順時針旋轉(zhuǎn)一定角度后,點B的對應(yīng)點恰好與點A重合,得到△ACE.
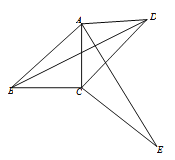
(1)求證:AE⊥BD;
(2)若AD=2,CD=3,試求四邊形ABCD的對角線BD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將三角形ABC先向右平移2個單位長度,再向下平移3個單位長度,得到對應(yīng)的三角形A1B1C1.
(1)求△ABC的面積;
(2)畫出三角形A1B1C1;
(3)寫出點A1、B1、C1的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】作圖題:
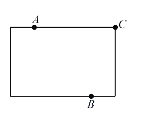
(1)為進一步打造“宜居北京”,某區(qū)擬在新竣工的矩形廣場的內(nèi)部修建一個音樂噴泉,要求音樂噴泉 ![]() 到廣場的兩個入口
到廣場的兩個入口 ![]() ,
,![]() 的距離相等,且到廣場管理處
的距離相等,且到廣場管理處 ![]() 的距離等于
的距離等于 ![]() 和
和 ![]() 之間距離的一半,
之間距離的一半,![]() ,
,![]() ,
,![]() 的位置如圖所示.請在答題卷的原圖上利用尺規(guī)作圖作出音樂噴泉
的位置如圖所示.請在答題卷的原圖上利用尺規(guī)作圖作出音樂噴泉 ![]() 的位置.(要求:不寫已知、求作、作法和結(jié)論,保留作圖痕跡,必須用鉛筆作圖)
的位置.(要求:不寫已知、求作、作法和結(jié)論,保留作圖痕跡,必須用鉛筆作圖)
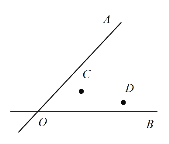
(2)如圖,兩條公路 ![]() 和
和 ![]() 相交于
相交于 ![]() 點,在
點,在 ![]() 的內(nèi)部有工廠
的內(nèi)部有工廠 ![]() 和
和 ![]() ,現(xiàn)要修建一個貨站
,現(xiàn)要修建一個貨站 ![]() ,使貨站
,使貨站 ![]() 到兩條公路
到兩條公路 ![]() ,
,![]() 的距離相等,且到兩工廠
的距離相等,且到兩工廠 ![]() ,
,![]() 的距離相等,用尺規(guī)作出貨站
的距離相等,用尺規(guī)作出貨站 ![]() 的位置.(要求:不寫作法,保留作圖痕跡,必須用鉛筆作圖)
的位置.(要求:不寫作法,保留作圖痕跡,必須用鉛筆作圖)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(閱讀)




如圖,點A是射線DM上的一個動點,以AD為邊作四邊形ABCD,且![]() ,
,![]() ,
,![]() ,
,![]() ,直線l經(jīng)過點D,且與四邊形的邊BC或BA相交,設(shè)直線l與DC的夾角
,直線l經(jīng)過點D,且與四邊形的邊BC或BA相交,設(shè)直線l與DC的夾角![]() ,將四邊形ABCD的直角
,將四邊形ABCD的直角![]() 沿直線l折疊,點C落在點
沿直線l折疊,點C落在點![]() 處,點B落在點
處,點B落在點![]() 處
處![]() 設(shè)AD的長為m.
設(shè)AD的長為m.
(理解)
若點![]() 與點A重合
與點A重合![]() 如圖
如圖![]() ,則
,則![]() ,
,![]() ;
;
(嘗試)
![]() 當(dāng)
當(dāng)![]() 時,若點
時,若點![]() 在四邊形ABCD的邊AB上
在四邊形ABCD的邊AB上![]() 如圖
如圖![]() ,求m的值;
,求m的值;
![]() 若點
若點![]() 恰為AB的中點
恰為AB的中點![]() 如圖
如圖![]() ,求
,求![]() 的度數(shù);
的度數(shù);
(探究)
![]() 作直線
作直線![]() ,與直線AD交于點G,與直線AB交于點H,當(dāng)
,與直線AD交于點G,與直線AB交于點H,當(dāng)![]() 與
與![]() 是一對相似的等腰三角形時,請直接寫出
是一對相似的等腰三角形時,請直接寫出![]() 及相對應(yīng)的m值.
及相對應(yīng)的m值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
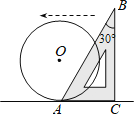
【題目】如圖,半徑為4的![]() 與含有
與含有![]() 角的真角三角板ABC的邊AC切于點A,將直角三角板沿CA邊所在的直線向左平移,當(dāng)平移到AB與
角的真角三角板ABC的邊AC切于點A,將直角三角板沿CA邊所在的直線向左平移,當(dāng)平移到AB與![]() 相切時,該直角三角板平移的距離為
相切時,該直角三角板平移的距離為![]()
![]()
A. 2 B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,AD是高,AE是角平分線,已知∠ACB = 70°,∠EAD = 15°,則∠ABC的度數(shù)為________
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com