
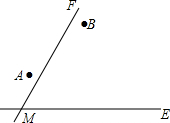
 兩個城鎮A、B與兩條公路ME,MF位置如圖所示,其中ME是東西方向的公路.現電信部門需在C處修建一座信號發射塔,要求發射塔到兩個城鎮A、B的距離必須相等,到兩條公路ME,MF的距離也必須相等,且在∠FME的內部
兩個城鎮A、B與兩條公路ME,MF位置如圖所示,其中ME是東西方向的公路.現電信部門需在C處修建一座信號發射塔,要求發射塔到兩個城鎮A、B的距離必須相等,到兩條公路ME,MF的距離也必須相等,且在∠FME的內部分析 (1)運用尺規作圖即可得出結果;
(2)作CD⊥MN于點D.由三角函數得出MD=$\sqrt{3}$CD,DN=$\frac{CD}{tan45°}$=CD,由已知條件得出$\sqrt{3}$CD+CD=2($\sqrt{3}$+1),解得CD=2km即可.
解答 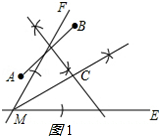 解:(1)答圖如圖1所示:
解:(1)答圖如圖1所示:
點C即為所求;
(2)作CD⊥MN于點D.如圖2所示:
∵在Rt△CMD中,∠CMN=30°,
∴$\frac{CD}{MD}$=tan∠CMN,
∴MD=$\frac{CD}{tan30°}$=$\frac{CD}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$CD,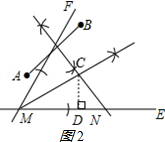 ∵在Rt△CND中,∠CNM=45°,$\frac{CD}{DN}$=tan∠CNM,
∵在Rt△CND中,∠CNM=45°,$\frac{CD}{DN}$=tan∠CNM,
∴DN=$\frac{CD}{tan45°}$=CD,∵MN=2($\sqrt{3}$+1)km,
∴MN=MD+DN=$\sqrt{3}$CD+CD=2($\sqrt{3}$+1)km.
解得:CD=2km.
答:點C到公路ME的距離為2km.
點評 本題考查了解直角三角形的應用、作圖-設計;熟練掌握基本作圖和解直角三角形是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 不賠不賺 | B. | 賺了8元 | C. | 賺了10元 | D. | 賺了32元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在直角坐標系中,一條拋物線與x軸交于A、B兩點,與y軸交于C點,其中B(3,0),C(0,4),點A在x軸的負半軸上,OC=4OA;
如圖,在直角坐標系中,一條拋物線與x軸交于A、B兩點,與y軸交于C點,其中B(3,0),C(0,4),點A在x軸的負半軸上,OC=4OA;查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2017屆江蘇省連云港市灌云縣西片九年級下學期第一次月考數學試卷(解析版) 題型:判斷題
如圖,小明同學用自制的直角三角形紙板DEF測量樹的高度AB,他調整自己的位置,設法使斜邊DF保持水平,并且邊DE與點B在同一直線上.已知紙板的兩條直角邊DE=40cm,EF=20cm,測得邊DF離地面的高度AC=1.5m,CD=8m,則樹高AB=__m.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com