
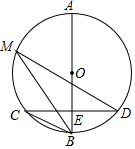
 如圖,已知AB是⊙O的直徑,弦CD⊥AB于點E,點M在⊙O上,∠M=∠D.
如圖,已知AB是⊙O的直徑,弦CD⊥AB于點E,點M在⊙O上,∠M=∠D.分析 (1)根據在同圓中,相等的圓周角所對的弧相等,相等的弧所對的圓周角相等,可以判斷出BC、MD的位置關系;
(2)根據垂徑定理和AE=16,BE=4,可以得到AB和OE的長度,然后根據勾股定理可以求得CE的長度,進而求得CD的長度.
解答 解:(1)BC、MD的位置關系是平行,
理由:∵∠M=∠D,
∴$\widehat{BD}=\widehat{MC}$,
∴∠M=∠MBC,
∴BC∥MD;
(2)連接OC,
∵AB是⊙O的直徑,弦CD⊥AB于點E,AE=16,BE=4,
∴∠OEC=90°,EC=ED,AB=AE+BE=20,
∴OC=10,OE=OB-BE=6,
∴CE=$\sqrt{O{C}^{2}-O{E}^{2}}=8$,
∴CD=2CE=16,
即線段CD的長是16.
點評 本題考查圓周角定理、垂徑定理、勾股定理,解題此類問題的關鍵是明確題意,根據所要證明或求解的問題找出相應的條件,利用圓周角定理、垂徑定理和勾股定理的相關知識解答.


科目:初中數學 來源: 題型:解答題
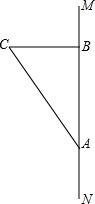 如圖所示線段中,A、B為南北方向高速公路MN的兩個出站口,A、B相距40km.風景區C在B的正西方向,司機小王由南向北到A后下高速路,沿老路AC到風景區C觀光旅游后,再沿C到B后發現從A→C→B共走了50km,但小王不知道從C到B有多少公里,你能用數學知識幫他解決這個問題嗎?請你寫出求解過程.
如圖所示線段中,A、B為南北方向高速公路MN的兩個出站口,A、B相距40km.風景區C在B的正西方向,司機小王由南向北到A后下高速路,沿老路AC到風景區C觀光旅游后,再沿C到B后發現從A→C→B共走了50km,但小王不知道從C到B有多少公里,你能用數學知識幫他解決這個問題嗎?請你寫出求解過程.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 記錄 | 天平左邊 | 天平右邊 | 天平狀態 |
| 記錄一 | 2枚1元硬幣和7枚5角硬幣 | 4個10克砝碼 | 平衡 |
| 記錄二 | 15枚1元硬幣 | 20枚5角硬幣和1個10克砝碼 | 平衡 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com