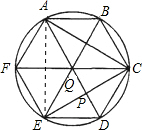
證明:(1)連AE,
∵AB=CD=EF,
∴弧AB=弧CD=弧EF,
∴∠AEB=∠CED,
∴∠QED=∠BEC+∠CED=∠BEC+∠AEB=∠AEC,
又∵∠QDE=∠ACE,
∴△QDE∽△ACE,
∴
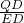
=

;
(2)∵弧CD=弧EF,
∴DE∥CF,
∴
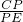
=
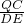
,∠CQD=∠QDE,
∵∠QED對BD弧,∠ADC對AC弧,
而DC弧=AB弧,
∴∠QED=∠ADC,
∴△QDC∽△DEQ,
∴
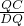
=

,即QC=
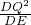
,
∴
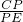
=
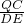
=
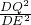
,
由(1)的結論
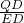
=

得,
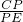
=
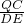
=
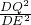
=
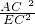
.
分析:(1)由AB=CD=EF,根據考查了在同圓或等圓中,如果兩個圓心角以及它們對應的兩條弧、兩條弦中有一組量相等,則另外兩組量也對應相等得到弧AB=弧CD=弧EF,得∠AEB=∠CED,得到∠QED=∠BEC+∠CED=∠BEC+∠AEB=∠AEC,則△QDE∽△ACE,即有
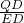
=

;
(2)由弧CD=弧EF,得到DE∥CF,則
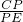
=
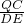
,∠CQD=∠QDE,而∠QED對BD弧,∠ADC對AC弧,所以∠QED=∠ADC,證得△QCD∽△DEQ,于是有
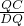
=

,即QC=
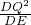
,得到
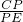
=
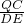
=
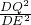
,再利用(1)的結論即可得到

.
點評:本題考查了在同圓或等圓中,如果兩個圓心角以及它們對應的兩條弧、兩條弦中有一組量相等,則另外兩組量也對應相等.也考查了三角形相似的判定與性質.

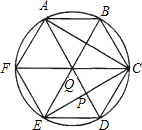
 如圖,圓內接六邊形ABCDEF滿足AB=CD=EF,且對角線AD、BE、CF相交于一點Q,設AD與CF的交點為P.
如圖,圓內接六邊形ABCDEF滿足AB=CD=EF,且對角線AD、BE、CF相交于一點Q,設AD與CF的交點為P. ;(2)
;(2) .
. 證明:(1)連AE,
證明:(1)連AE,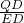 =
= ;
;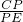 =
=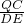 ,∠CQD=∠QDE,
,∠CQD=∠QDE,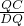 =
= ,即QC=
,即QC=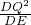 ,
,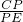 =
=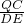 =
=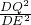 ,
,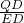 =
= 得,
得,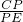 =
=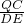 =
=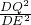 =
=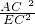 .
.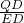 =
= ;
;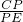 =
=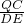 ,∠CQD=∠QDE,而∠QED對BD弧,∠ADC對AC弧,所以∠QED=∠ADC,證得△QCD∽△DEQ,于是有
,∠CQD=∠QDE,而∠QED對BD弧,∠ADC對AC弧,所以∠QED=∠ADC,證得△QCD∽△DEQ,于是有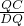 =
= ,即QC=
,即QC=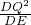 ,得到
,得到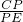 =
=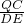 =
=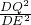 ,再利用(1)的結論即可得到
,再利用(1)的結論即可得到 .
.

 應用題作業本系列答案
應用題作業本系列答案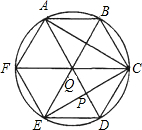 如圖,圓內接六邊形ABCDEF滿足AB=CD=EF,且對角線AD、BE、CF相交于一點Q,設AD與CF的交點為P.
如圖,圓內接六邊形ABCDEF滿足AB=CD=EF,且對角線AD、BE、CF相交于一點Q,設AD與CF的交點為P.