
 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:初中數學 來源: 題型:選擇題
 如圖,大拇指與小拇指盡量張開時,兩指尖的距離稱為指距.根據最近人體構造學的研究成果表明,一般情況下人的指距d和身高h成某種關系.如表是測得的指距與身高的一組數據:
如圖,大拇指與小拇指盡量張開時,兩指尖的距離稱為指距.根據最近人體構造學的研究成果表明,一般情況下人的指距d和身高h成某種關系.如表是測得的指距與身高的一組數據:| 指距d(cm) | 20 | 21 | 22 | 23 |
| 身高h(cm) | 160 | 169 | 178 | 187 |
| A. | 25.3厘米 | B. | 26.3厘米 | C. | 27.3厘米 | D. | 28.3厘米 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,已知P是兩直角邊分別為3cm、4cm的Rt△ABC斜邊AB上的任意一點,以CP為直徑作圓,則該圓的面積y(cm2)與CP的長x(cm)之間的函數關系式是y=$\frac{1}{4}$πx2,自變量x的取值范圍是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.
如圖,已知P是兩直角邊分別為3cm、4cm的Rt△ABC斜邊AB上的任意一點,以CP為直徑作圓,則該圓的面積y(cm2)與CP的長x(cm)之間的函數關系式是y=$\frac{1}{4}$πx2,自變量x的取值范圍是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
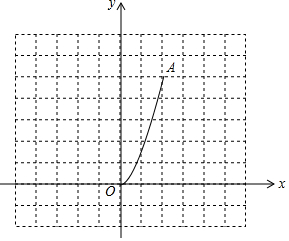 如圖,二次函數y=$\frac{5}{4}$x2(0≤x≤2)的圖象記為曲線C1,將C1繞坐標原點O逆時針旋轉90°,得曲線C2.
如圖,二次函數y=$\frac{5}{4}$x2(0≤x≤2)的圖象記為曲線C1,將C1繞坐標原點O逆時針旋轉90°,得曲線C2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com