
某家電生產企業根據市場調查分析,決定調整產品生產方案,準備每周(按120個工時計算)生產空調、冰箱、彩電共360臺,且彩電至少生產60臺,已知生產這些家電產品每臺所需工時和每臺產值如下表:
| 家電名稱 | 空調 | 冰箱 | 彩電 |
| 工時 |
|
|
|
| 產值(千元) | 4 | 3 | 2 |
問每周應生產空調、冰箱、彩電各多少臺,才能使產值最高?最高產值是多少?
設每周應生產空調x臺,冰箱y臺,則生產彩電(360—x—y)臺………(2分)
由每周工時可知: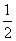 x+
x+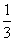 y+
y+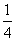 (360—x—y)=120………………………………………(3分)
(360—x—y)=120………………………………………(3分)
整理可得,y=360—3x,360—x—y=2x……………………………………………(4分)
不妨設每周產值為W,則W=4x+3y+2( 360—x—y)=1080-x……………………(5分)
360—x—y)=1080-x……………………(5分)
另據360—3x≥0,2x≥60,得30≤x≤120 且x為整數……………………………(6分)
且x為整數……………………………(6分)
注意到W是關于x的一次函數,且W隨x的增大而減小,當x=30時,W有最大值,
W最大=1080-30=1050,……………………………………………………………(7分)
故每周生產空調30臺,冰箱270臺,彩電60臺時,能創最高產值1050千元…(8分)
【其它正確解法,分步酌情給分】


 目標測試系列答案
目標測試系列答案科目:初中數學 來源: 題型:
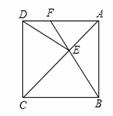
如圖,正方形ABCD中,點E在對角線AC上,連接EB、ED.
(1)求證:△BCE≌△DCE;
(2)延長BE交AD于點F,若∠DEB=140º,求∠AFE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,矩形ABCD中,E為AD中點,點F為BC上的動點(不
如圖,矩形ABCD中,E為AD中點,點F為BC上的動點(不
與B、C重合).連接EF,以EF為直徑的圓分別交BE,CE
于點G、H. 設BF的長度為x,弦FG與FH的長度和為y,則
下列圖象中,能表示y與x之間的函數關系的圖象大致是

A B C D
查看答案和解析>>
科目:初中數學 來源: 題型:
已知:關于 的一元二次方程
的一元二次方程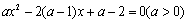 .
.
(1)求證:方程有兩個不相等的實數根;
(2)設方程的兩個實數根分別為 ,
, (其中
(其中 >
> ).若
).若 是關于
是關于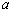 的函數,且
的函數,且
 ,求這個函數的表達式;
,求這個函數的表達式;
(3)在(2)的條件下,結合函數的圖象回答:若使 ,則自變量
,則自變量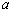 的取值范圍為 .
的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山西農業大學附屬中學八年級上學期期末考試數學試卷(解析版) 題型:填空題
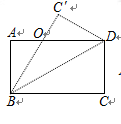
如圖所示,△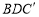 是將長方形紙牌ABCD沿著BD折疊得到的,圖中(包括實線、虛線在內)共有全等三角形 對。
是將長方形紙牌ABCD沿著BD折疊得到的,圖中(包括實線、虛線在內)共有全等三角形 對。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com