
 在Rt△ABC中,∠ACB=Rt∠,M是邊AB的中點,CH⊥AB于點H,CD平分∠ACB.
在Rt△ABC中,∠ACB=Rt∠,M是邊AB的中點,CH⊥AB于點H,CD平分∠ACB.分析 (1)根據(jù)直角三角形斜邊上的中線等于斜邊的一半得到AM=CM=BM,由等腰三角形到性質(zhì)得到∠CAB=∠ACM,由余角的性質(zhì)得到∠CAB=∠BCH,等量代換得到∠BCH=∠ACM,根據(jù)角平分線的性質(zhì)得到∠ACD=∠BCD,即可得到結(jié)論;
(2)根據(jù)EM⊥AB,CH⊥AB,得到EM∥AB,由平行線的性質(zhì)得到∠HCD=∠MED,由于∠HCD=∠MCD,于是得到∠MCD=∠MED,即可得到結(jié)論;
(3)根據(jù) CM=EM AM=CM=BM,于是得到EM=AM=BM,推出△AEB是直角三角形,由于 EM垂直平分AB,得到EA=EB于是得到結(jié)論.
解答 證明:(1)Rt△ABC中,∠ACB=90°,
∵M是AB邊的中點,
∴AM=CM=BM,
∴∠CAB=∠ACM,
∴∠CAB=90-∠ABC,
∵CH⊥AB,
∴∠BCH=90-∠ABC,
∴∠CAB=∠BCH,
∴∠BCH=∠ACM,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ACD-∠ACM=∠BCD-∠BCH,
即∠MCD=∠HCD,
∴CD平分∠MCH;
(2)∵EM⊥AB,CH⊥AB,
∴EM∥CH,
∴∠HCD=∠MED,
∵∠HCD=∠MCD,
∴∠MCD=∠MED,
∴CM=EM;
(3)△AEB是等腰直角三角形,
∵CM=EM AM=CM=BM,
∴EM=AM=BM,
∴△AEB是直角三角形,
∵EM垂直平分AB,
∴EA=EB,
∴△AEB是等腰三角形,
∴△AEB是等腰直角三角形.
點評 本題考查了直角三角形斜邊上的中線等于斜邊的一半,等腰直角三角形的判定和性質(zhì),角平分線的定義,線段垂直平分線的性質(zhì),等腰三角形的性質(zhì),熟練掌握各定理是解題的關(guān)鍵.


科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
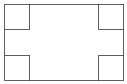 如圖所示,在長和寬分別是a、b的矩形紙片的四個角上都剪去一個邊長為x的小正方形,折成一個無蓋的紙盒.
如圖所示,在長和寬分別是a、b的矩形紙片的四個角上都剪去一個邊長為x的小正方形,折成一個無蓋的紙盒.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\frac{5}{2}<r<4$ | B. | $\frac{5}{2}<r<3$ | C. | 3<r<4 | D. | r>3 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com