
分析 (1)根據點A、B的坐標利用待定系數法即可求出這個函數的解析式;
(2)根據一次函數圖象上點的坐標特征即可求出兩直線的交點坐標,再根據點的坐標利用待定系數法即可求出這條直線的解析式.
解答 解:(1)將A(1,1)、B(2,3)代入y=kx+b,
$\left\{\begin{array}{l}{k+b=1}\\{2k+b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
∴這個函數的解析式為y=2x-1.
(2)設這條直線的解析式為y=mx+n(m≠0),
當x=-2時,y=2x-1=-5,
∴兩直線的交點坐標為(-2,-5).
將(-2,-5)、(0,5)代入y=mx+n,
$\left\{\begin{array}{l}{-2m+n=-5}\\{n=5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=5}\\{n=5}\end{array}\right.$,
∴這條直線的解析式為y=5x+5.
點評 本題考查了待定系數法求一次函數解析式以及一次函數圖象上點的坐標特征,能夠熟練運用待定系數法求出函數解析式是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
 連接邊長為1的正方形對邊中點,可將一個正方形分成四個全等的小正方形,選右下角的小正方形進行第二次操作,又可將這個小正方形分成四個更小的小正方形,…重復這樣的操作,則2016次操作后右下角的小正方形面積是( )
連接邊長為1的正方形對邊中點,可將一個正方形分成四個全等的小正方形,選右下角的小正方形進行第二次操作,又可將這個小正方形分成四個更小的小正方形,…重復這樣的操作,則2016次操作后右下角的小正方形面積是( )| A. | $\frac{1}{2004}$ | B. | ${(\frac{1}{2})^{2016}}$ | C. | ${(\frac{1}{4})^{2016}}$ | D. | $1-{(\frac{1}{4})^{2016}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
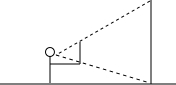 如圖,一個人拿著一把厘米刻度尺,站山在距電線桿30m的地方,把甲臂向前伸直,刻度尺豎直,尺上0-12cm這一段恰好遮住電線桿.若手臂的長為60cm.求電線桿的高度.
如圖,一個人拿著一把厘米刻度尺,站山在距電線桿30m的地方,把甲臂向前伸直,刻度尺豎直,尺上0-12cm這一段恰好遮住電線桿.若手臂的長為60cm.求電線桿的高度.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,直線AC、DF被三條平行線l1,l2,l3所截,交點分別為A,D,B,E,C,F,且AB=3,BC=5,EF=4,則DE=$\frac{12}{5}$.
如圖,直線AC、DF被三條平行線l1,l2,l3所截,交點分別為A,D,B,E,C,F,且AB=3,BC=5,EF=4,則DE=$\frac{12}{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com