Question

3．把圖1的矩形紙片ABCD折疊，B、C兩點(diǎn)恰好重合落在AD邊上的點(diǎn)P處（如圖2）已知∠MPN=90°，PM=3，PN=4．

（1）MN=5；（2）矩形紙片ABCD的面積為28.8．

Answer 1

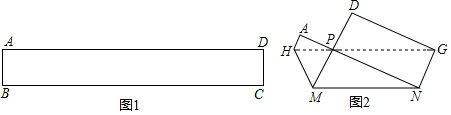
分析 （1）由勾股定理求出MN即可；
（2）根據(jù)折疊的性質(zhì)，得BC的長(zhǎng)即為MP+MN+NP=12，再由三角形面積求出PF，得出AB的長(zhǎng)，即可求出矩形的面積．

解答 解：（1）∵∠MPN=90°，PM=3，PN=4，
∴MN=$\sqrt{{3}^{2}+{4}^{2}}$=5；
故答案為：5；
（2）BC=MP+MN+NP=12，
作PF⊥MN于F，如圖所示：
則AB=PF=$\frac{PM•PN}{MN}$=2.4，
則長(zhǎng)方形紙片ABCD的面積=AB•BC=28.8，
故答案為：28.8．

點(diǎn)評(píng) 此題主要考查了折疊的性質(zhì)、勾股定理以及直角三角形的面積公式，利用直角三角形兩條直角邊的乘積除以斜邊得斜邊的高是解答此題的關(guān)鍵．