
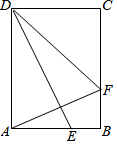
 在矩形ABCD中,BC=10cm、DC=6cm,點E、F分別為邊AB、BC上的兩個動點,E從點A出發以每秒5cm的速度向B運動,F從點B出發以每秒3cm的速度向C運動,設運動時間為t秒.若∠AFD=∠AED,則t的值為( )
在矩形ABCD中,BC=10cm、DC=6cm,點E、F分別為邊AB、BC上的兩個動點,E從點A出發以每秒5cm的速度向B運動,F從點B出發以每秒3cm的速度向C運動,設運動時間為t秒.若∠AFD=∠AED,則t的值為( )| A. | $\sqrt{2}-1$ | B. | 0.5 | C. | $\frac{2}{3}$ | D. | 1 |
分析 根據題意知AE=5t、BF=3t,由$\frac{AE}{AD}$=$\frac{t}{2}$=$\frac{BF}{AB}$且∠DAE=∠ABF=90°證△ADE∽△BAF得∠2=∠3,結合∠3=∠4、∠1=∠2得∠1=∠4,即可知DF=DA,從而得62+(10-3t)2=102,解之可得t的值,繼而根據0≤5t≤6且0≤3t≤10取舍可得答案.
解答 解:如圖,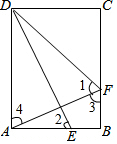
根據題意知,AE=5t,BF=3t,
∵BC=10cm,DC=6cm,
∴$\frac{AE}{AD}$=$\frac{5t}{10}$=$\frac{t}{2}$,$\frac{BF}{AB}$=$\frac{3t}{6}$=$\frac{t}{2}$,
∴$\frac{AE}{AD}=\frac{BF}{AB}$,
又∵∠DAE=∠ABF=90°,
∴△ADE∽△BAF,
∴∠2=∠3,
∵AD∥BC,
∴∠3=∠4,
∴∠2=∠4,
∵∠1=∠2,
∴∠1=∠4,
∴DF=DA,即DF2=AD2,
∵BF=3t,BC=10,
∴CF=10-3t,
∴DF2=DC2+CF2,即DF2=62+(10-3t)2,
∴62+(10-3t)2=102,
解得:t=$\frac{2}{3}$或t=6,
∵0≤5t≤6且0≤3t≤10,
∴0≤t≤$\frac{6}{5}$,
∴t=$\frac{2}{3}$,
故選:C.
點評 本題主要考查相似三角形的判定與性質、勾股定理、等角對等邊和矩形的性質等知識點,根據對應邊成比例且夾角相等得出兩三角形相似繼而由等角對等邊得出關于t的方程是解題的關鍵.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源:2017屆江蘇省無錫市九年級3月月考數學試卷(解析版) 題型:判斷題
如圖,四邊形ABCD 內接于⊙O,BD是⊙O的直徑,過點A作⊙O的切線AE交CD的延長線于點E,DA平分∠BDE.
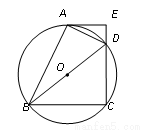
(1)求證:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
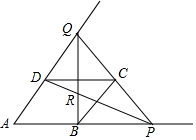 如圖,四邊形ABCD是邊長為a的菱形,且∠A=60°,P是AB延長線上一動點,聯結PC并延長交AD的延長線于點Q,聯結BQ交PD于點R
如圖,四邊形ABCD是邊長為a的菱形,且∠A=60°,P是AB延長線上一動點,聯結PC并延長交AD的延長線于點Q,聯結BQ交PD于點R查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com