
 如圖,拋物線y=ax2-8ax(a>0)與x軸交于O,A兩點,它的頂點為P,經過O,A兩點的圓⊙M與y軸交于點B,拋物線的對稱軸與⊙M交于點C,連接AB,BP,當CD:DM:CP=2:3:4時,tan∠ABP的值是$\frac{9}{13}$.
如圖,拋物線y=ax2-8ax(a>0)與x軸交于O,A兩點,它的頂點為P,經過O,A兩點的圓⊙M與y軸交于點B,拋物線的對稱軸與⊙M交于點C,連接AB,BP,當CD:DM:CP=2:3:4時,tan∠ABP的值是$\frac{9}{13}$. 分析 求出OA=8,OD=AD=4,設CD=2x,DM=3x,CP=4x,則⊙M的半徑為2x+3x=5x,AM=5x,根據勾股定理求出x,求出CD=2,DM=3,CP=4,PE=5+5+4=14,連接BE、CF,作BN⊥CD于N,求出BN=OD=4,MN=DM=3,PN=12,根據勾股定理求出PB,求出△PCF∽△PBE,根據比例式求出PF,求出BF,根據勾股定理求出AF,解直角三角形求出即可.
解答 解:∵物線y=ax2-8ax(a>0)與x軸交于O,A兩點,
∴ax2-8ax=0,
解得:x=0或8,
即OA=8,
∵CD為對稱軸,
∴CD⊥OA且平分OA,
∴OD=AD=4,
∵CD:DM:CP=2:3:4,
∴設CD=2x,DM=3x,CP=4x,則⊙M的半徑為2x+3x=5x,AM=5x,
在Rt△MDA中,由勾股定理得:(3x)2+42=(5x)2,
解得:x=1,
即CD=2,DM=3,CP=4,PE=5+5+4=14,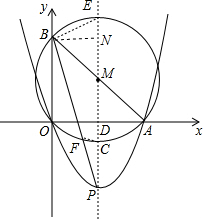
如圖,連接BE、CF,作BN⊥CD于N,
則BN=OD=4,MN=DM=3,PN=12,
由勾股定理得:PB=$\sqrt{P{N}^{2}+B{N}^{2}}$=4$\sqrt{10}$,
∵點B、F、C、E在⊙M上,
∴∠PCF=∠PBE,
∵∠FPC=∠BPE,
∴△PCF∽△PBE,
∴$\frac{PC}{PB}$=$\frac{PF}{PE}$,
∴PF=$\frac{4×14}{4\sqrt{10}}$=$\frac{7\sqrt{10}}{5}$,
∴BF=PB-PF=4$\sqrt{10}$-$\frac{7}{5}$$\sqrt{10}$=$\frac{13}{5}$$\sqrt{10}$,
∵AF2=AB2-BF2=100-$\frac{338}{5}$=$\frac{162}{5}$,
∴AF=$\frac{9}{5}$$\sqrt{10}$,
∴在Rt△ABF中,tan∠ABF=$\frac{AF}{BF}$=$\frac{\frac{9}{5}\sqrt{10}}{\frac{13}{5}\sqrt{10}}$=$\frac{9}{13}$,
故答案為:$\frac{9}{13}$.
點評 本題考查了拋物線與x軸的交點,二次函數的性質,相似三角形的性質和判定,解直角三角形等知識點,能綜合運用知識點進行計算是解此題的關鍵.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{-x}{-x-y}$ | B. | $\frac{x}{x-y}$ | C. | -$\frac{x}{x-y}$ | D. | -$\frac{x}{y-x}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,直線y=$\frac{3}{4}$x-$\frac{3}{2}$與拋物線y=-$\frac{1}{4}$x2+bx+c交于A、B兩點,點A在x軸上,點B的橫坐標為-8.
如圖,在平面直角坐標系中,直線y=$\frac{3}{4}$x-$\frac{3}{2}$與拋物線y=-$\frac{1}{4}$x2+bx+c交于A、B兩點,點A在x軸上,點B的橫坐標為-8.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 九個邊長為1的正方形如圖擺放在平面直角坐標系中,經過原點的一條直線l將這九個正方形分成面積相等的兩部分,則該直線l的函數關系式是y=-$\frac{9}{11}$x.
九個邊長為1的正方形如圖擺放在平面直角坐標系中,經過原點的一條直線l將這九個正方形分成面積相等的兩部分,則該直線l的函數關系式是y=-$\frac{9}{11}$x.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2017屆湖南津市中考數學模擬試卷(2)(解析版) 題型:解答題
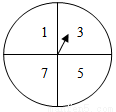
A超市在一次周年慶典當天開展購物抽獎活動,凡當天在該超市購物的顧客,均有一次抽獎機會,抽獎規則如下:將如圖所示的圖形轉盤平均分成四個扇形,分別標上1,3,5,7四個數字,抽獎者連續轉動轉盤兩次,當每次停止后指針所指扇形內的數為每次所得數(若指針指在分界處重轉),當兩次所得數字之和為2時,返現金20元,當兩次所得數字之和為4時,返現金10元,當兩次所得數字之和為6時,返現金5元.
(1)試用樹狀圖或列表的方法,表示出王大媽這次抽獎中所有可能出現的結果.
(2)試求王大媽在參加這次抽獎活動中,能獲得返現金的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com