Question

7．如圖，AB是⊙O的直徑，CD與⊙O相切于點C，∠BCD=∠CBD，BD交AC的延長線于點E．
（1）求證：BE與⊙O相切；
（2）若tan∠ABC=$\frac{4}{3}$，半徑r=2，求CE的長．

Answer 1

分析 （1）欲證明BE是切線，只要證明∠OBE=90°即可．
（2）由△EBC∽△BAC，得到BC：AC=EC：BC，即BC²=CE•CA，由tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$，設，AC=4k，BC=3k，推出CE=$\frac{9}{4}$k，在Rt△ABC中，根據AB²=BC²+AC²，
列出方程求出k即可解決問題．

解答 （1）證明：如圖連接OC．
∵CD是切線，
∴OC⊥CD，
∴∠COD=90°，
∵OC=OB，
∴∠OCB=∠OBC，∵∠DCB=∠DBC，
∴∠DCB+∠OCB=∠DBC+∠OBC=90°，
∴∠DBO=90°，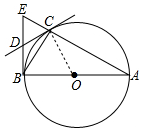
∴OB⊥EB，'
∴BE是⊙O的切線．

（2）解：∵AB是直徑，
∴∠BCA=∠ECB=90°，
∵∠A+∠ABC=90°，∠EBC+∠ABC=90°，
∴∠EBC=∠A，
∴△EBC∽△BAC，
∴BC：AC=EC：BC，
∴BC²=CE•CA，
∵tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$，設，AC=4k，BC=3k，
∴CE=$\frac{9}{4}$k，
在Rt△ABC中，∵AB²=BC²+AC²，
∴4=25k²，
∵k＞0，
∴k=$\frac{2}{5}$，
∴EC=$\frac{9}{4}$×$\frac{2}{5}$=$\frac{9}{10}$．

點評 本題考查切線的判定、直徑的性質、等腰三角形的性質、相似三角形的判定和性質、銳角三角函數、勾股定理等知識，解題的關鍵是靈活運用所學知識，學會利用參數解決問題，屬于中考常考題型．