
類比、轉化、分類討論等思想方法和數學基本圖形在數學學習和解題中經常用到,如下是一個案例,請補充完整。
原題:如圖1,在⊙O中,MN是直徑,AB⊥MN于點B,CD⊥MN于點D,∠AOC=90°,AB=3,CD=4,則BD= 。
⑴嘗試探究:如圖2,在⊙O中,MN是直徑,AB⊥MN于點B,CD⊥MN于點D,點E在MN上,∠AEC=90°,AB=3,BD=8,BE:DE=1:3,則CD= (試寫出解答過程)。
⑵類比延伸:利用圖3,再探究,當A、C兩點分別在直徑MN兩側,且AB≠CD,AB⊥MN于點B,CD⊥MN于點D,∠AOC=90°時,則線段AB、CD、BD滿足的數量關系為 。
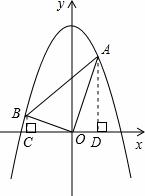
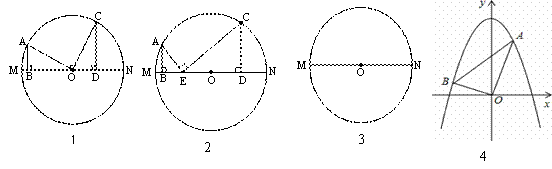 ⑶拓展遷移:如圖4,在平面直角坐標系中,拋物線經過A(m,6),B(n,1)兩點(其中0<m<3),且以y軸為對稱軸,且∠AOB=90°,①求mn的值;②求拋物線的解析式。
⑶拓展遷移:如圖4,在平面直角坐標系中,拋物線經過A(m,6),B(n,1)兩點(其中0<m<3),且以y軸為對稱軸,且∠AOB=90°,①求mn的值;②求拋物線的解析式。
解:原題:∵AB⊥MN,CD⊥MN,
∴∠ABO=∠ODC=90° ∠BAO+∠AOB=90°
∵∠AOC=90° ∴∠DOC+∠AOB=90°
∴∠BAO=∠DOC 又∵OA=OC ∴△AOB≌△ODC(AAS)
∴OD=AB=3,OB=CD=4,∴BD=OB+OD=7
 |
嘗試探究:∵AB⊥MN,CD⊥MN,∴∠ABE=∠CDE=90°
∠BAE+∠AEB=90°∵∠AEC=90°∴∠DEC+∠AEB=90°
∴∠BAE=∠DEC ∴△ABE∽△EDC
∴
∵AB=3,BD=8,BE:DE=1:3,
∴BE=2,DE=6 ∴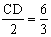 ∴CD=4
∴CD=4
⑵類比延伸:
如圖3(a)CD=AB+BD;
 如圖3(b)AB=CD+BD
如圖3(b)AB=CD+BD
 |
⑶拓展遷移:
① 作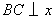 軸于C點,
軸于C點,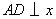 軸于D點,
軸于D點,
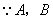 點坐標分別為
點坐標分別為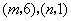 ,
,
∴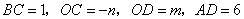 ,又∵∠AOB=90°
,又∵∠AOB=90°
∴∠BCO=∠ODA=90°,∠OBC=∠AOD
∴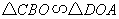 ,
,
∴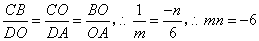 。
。
②由①得,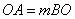 ,又
,又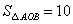 ,∴
,∴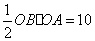 ,
,
即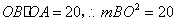 ,
,
又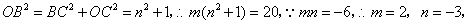
∴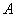 坐標為(2,6),B坐標為(-3,1),
坐標為(2,6),B坐標為(-3,1),
代入得拋物線解析式為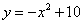


科目:初中數學 來源: 題型:
)為迎接中國森博會,某商家計劃從廠家采購A,B兩種產品共20件,產品的采購單價(元/件)是采購數量(件)的一次函數,下表提供了部分采購數據.
| 采購數量(件) | 1 | 2 | … |
| A產品單價(元/件) | 1480 | 1460 | … |
| B產品單價(元/件) | 1290 | 1280 | … |
(1)設A產品的采購數量為x(件),采購單價為y1(元/件),求y1與x的關系式;
(2)經商家與廠家協商,采購A產品的數量不少于B產品數量的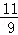 ,且A產品采購單價不低于1200元,求該商家共有幾種進貨方案;
,且A產品采購單價不低于1200元,求該商家共有幾種進貨方案;
(3)該商家分別以1760元/件和1700元/件的銷售單價售出A,B兩種產品,且全部售完,在(2)的條件下,求采購A種產品多少件時總利潤最大,并求最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
將二次函數 的圖象先向右平移一個單位,再沿x軸翻折到第一象限,然后向右平移一個單位,再沿y軸翻折到第二象限…以此類推,如果把向右平移一個單位再沿坐標軸翻折一次記作1次變換,那么二次函數
的圖象先向右平移一個單位,再沿x軸翻折到第一象限,然后向右平移一個單位,再沿y軸翻折到第二象限…以此類推,如果把向右平移一個單位再沿坐標軸翻折一次記作1次變換,那么二次函數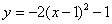 的圖象經過2013次變換后,得到的圖象的函數解析式為 .
的圖象經過2013次變換后,得到的圖象的函數解析式為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
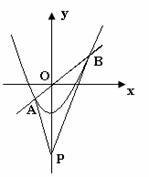
如圖在平面直角坐標系xOy中,直線y=kx(k為常數)與拋物線
 交于A,B兩點,且A點在y軸左側,P點坐標為(0,-4),
交于A,B兩點,且A點在y軸左側,P點坐標為(0,-4),
連接PA,PB.以下說法正確的是( )
① 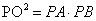 ;② 當k>0時,(PA+AO)(PB-BO)的值隨k的增大而增大;③ 當
;② 當k>0時,(PA+AO)(PB-BO)的值隨k的增大而增大;③ 當 時,
時,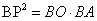 ;④三角形PAB面積的最小值為
;④三角形PAB面積的最小值為 .
.
 A.③④ B.①②
A.③④ B.①② C.②④ D.①④
C.②④ D.①④
查看答案和解析>>
科目:初中數學 來源: 題型:
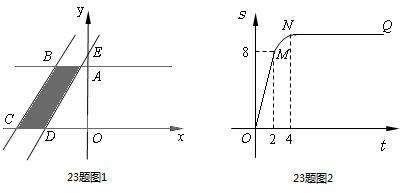
如圖1所示,直角梯形OABC的頂點A、C分別在y軸正半軸與 軸負半軸上.過點B、C作直線
軸負半軸上.過點B、C作直線 .將直線
.將直線 平移,平移后的直線
平移,平移后的直線 與
與 軸交于點D,與
軸交于點D,與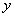 軸交于點E.
軸交于點E.
(1)將直線 向右平移,設平移距離CD為
向右平移,設平移距離CD為 (t
(t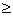 0),直角梯形OABC被直線
0),直角梯形OABC被直線 掃過的面積(圖中陰影部份)為
掃過的面積(圖中陰影部份)為 ,
, 關于
關于 的函數圖象如圖2所示, OM為線段,MN為拋物線的一部分,NQ為射線,N點橫坐標為4.
的函數圖象如圖2所示, OM為線段,MN為拋物線的一部分,NQ為射線,N點橫坐標為4.
①求梯形上底AB的長及直角梯形OABC的面積; ②求S關于 的函數解析式;
的函數解析式;
(2)在第(1)題的條件下,當直線 向左或向右平移時(包括
向左或向右平移時(包括 與直線BC重合),在直線AB上是否存在點P,使
與直線BC重合),在直線AB上是否存在點P,使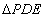 為等腰直角三角形?若存在,請直接寫出所有滿足條件的點P的坐標;若不存在,請說明理由.
為等腰直角三角形?若存在,請直接寫出所有滿足條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com