）為迎接中國森博會，某商家計劃從廠家采購A，B兩種產品共20件，產品的采購單價（元/件）是采購數量（件）的一次函數，下表提供了部分采購數據．
| 采購數量（件） | 1 | 2 | … |
| A產品單價（元/件） | 1480 | 1460 | … |
| B產品單價（元/件） | 1290 | 1280 | … |
（1）設A產品的采購數量為x（件），采購單價為y1（元/件），求y1與x的關系式；
（2）經商家與廠家協商，采購A產品的數量不少于B產品數量的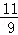
，且A產品采購單價不低于1200元，求該商家共有幾種進貨方案；
（3）該商家分別以1760元/件和1700元/件的銷售單價售出A，B兩種產品，且全部售完，在（2）的條件下，求采購A種產品多少件時總利潤最大，并求最大利潤．
培優好卷單元加期末卷系列答案
一線名師權威作業本系列答案科目：初中數學 來源： 題型：
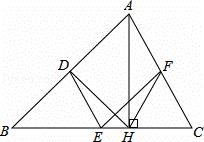
如圖，在△ABC中，點D，E，F分別是AB，BC，CA的中點，AH是邊BC上的高．
（1）求證：四邊形ADEF是平行四邊形；
（2）求證：∠DHF=∠DEF．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，直角三角板ABC的斜邊AB＝12 cm，∠A＝30°，將三角板ABC繞C順時針旋轉90°至三角板A′B′C′的位置后，再沿CB方向向左平移，使點B′落在原三角板ABC的斜邊AB上，則三角板A′B′C′平移的距離為
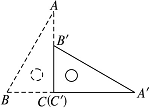
查看答案和解析>>
科目：初中數學 來源： 題型：
對非負實數x “四舍五入”到個位的值記為<x>，即當n為非負整數時，若n－
≤x <n+ ,則<x>=n,如<0.46>=0,<3.67>=4,給出下列關于<x>的結論： ① <1.493>=1, ② <2x>=2<x>, ③ 若<x－1>=4，則實數x的取值范圍是9≤x<11, ④ 當x≥0，m為非負整數時，有<m+2013x >= m+<2013x>, ⑤ <x+y>=<x>+<y>. 其中，正確的結論有（ ）個。
A、2個 B、3個 C、4個 D、5個
查看答案和解析>>
科目：初中數學 來源： 題型：
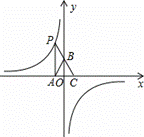如圖，點P是反比例函數
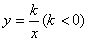圖象上的點，PA垂直
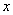軸于點A（－1，0），點C的坐標為（1，0），PC交
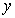軸于點B，連結AB，已知AB=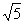
（1）
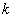的值是__________；
（2）若M（
，
）是該反比例函數圖象上的點，且滿足
∠MBA<∠ABC,則的取值范圍是__________
查看答案和解析>>
科目：初中數學 來源： 題型：
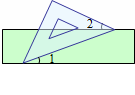
如圖，把一塊含有45°角的直角三角板的兩個頂點放在直尺的對邊上．如果∠1=15°，則∠2的度數是（ ）
A．30° B．25° C．35° D．20°
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，AB為等腰直角⊿ABC的斜邊（AB為定長線段），O為AB的中點，P為AC延長線上的一個動點，線段PB的垂直平分線交線段OC于點E，D為垂足，當P點運動時，給出下列四個結論，其中正確的個數是( )
①E為⊿ABP的外心； ②∠PEB=90°；
③PC·BE = OE·PB； ④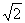
CE + PC=
．
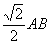A．1個 B．2個 C．3個 D．4個
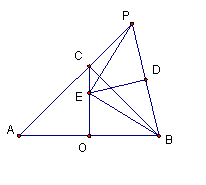
查看答案和解析>>
科目：初中數學 來源： 題型：
類比、轉化、分類討論等思想方法和數學基本圖形在數學學習和解題中經常用到，如下是一個案例，請補充完整。
原題：如圖1，在⊙O中，MN是直徑，AB⊥MN于點B，CD⊥MN于點D，∠AOC=90°，AB=3，CD=4，則BD= 。
⑴嘗試探究：如圖2，在⊙O中，MN是直徑，AB⊥MN于點B，CD⊥MN于點D，點E在MN上，∠AEC=90°，AB=3，BD=8，BE：DE=1:3，則CD= （試寫出解答過程）。
⑵類比延伸：利用圖3，再探究，當A、C兩點分別在直徑MN兩側，且AB≠CD，AB⊥MN于點B，CD⊥MN于點D，∠AOC=90°時，則線段AB、CD、BD滿足的數量關系為 。
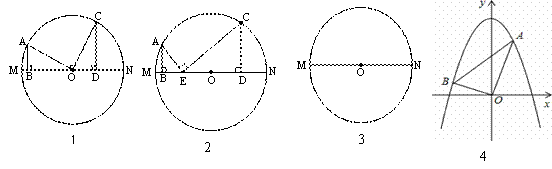⑶拓展遷移：如圖4，在平面直角坐標系中，拋物線經過A（m，6），B（n，1）兩點（其中0＜m＜3），且以y軸為對稱軸，且∠AOB=90°，①求mn的值；②求拋物線的解析式。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
，
的值等于（ ）
B. 
C . 
D . 