
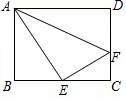
 如圖,在矩形ABCD中,AB=6,BC=8,點E是BC中點,點F是邊CD上的任意一點,當△AEF的周長最小時,則cos∠EAF=$\frac{7\sqrt{65}}{65}$.
如圖,在矩形ABCD中,AB=6,BC=8,點E是BC中點,點F是邊CD上的任意一點,當△AEF的周長最小時,則cos∠EAF=$\frac{7\sqrt{65}}{65}$. 分析 作點E關于直線CD的對稱點E′,連接AE′交CD于點F,作EH⊥AF于H.,再根據△CEF∽△BEA即可求出CF的長,進而得出DF的長,想辦法求出AE、AH,即可求出cos∠EAF的值.
解答 解:作點E關于直線CD的對稱點E′,連接AE′交CD于點F,作EH⊥AF于H.
∵在矩形ABCD中,AB=6,BC=8,點E是BC中點,
∴BE=CE=CE′=4,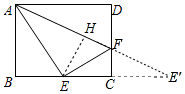
∵AB⊥BC,CD⊥BC,
∴$\frac{CE'}{BE'}=\frac{CF}{AB}$,即$\frac{4}{8+4}=\frac{CF}{6}$,解得CF=2,
∴DF=CD-CF=6-2=4.
∴AE=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,AF=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∵S△AEF=$\frac{1}{2}$•AF•EH=S矩形ABCD-S△ABE-S△ADF-S△EFC,
∴$\frac{1}{2}$$•4\sqrt{5}$•EH=16,
∴EH=$\frac{8\sqrt{5}}{5}$,
在Rt△AEH中,AH=$\sqrt{A{E}^{2}-E{H}^{2}}$=$\sqrt{(2\sqrt{13})^{2}-(\frac{8\sqrt{5}}{5})^{2}}$=$\frac{14\sqrt{5}}{5}$,
∴cos∠EAF=$\frac{AH}{AE}$=$\frac{\frac{14\sqrt{5}}{5}}{2\sqrt{13}}$=$\frac{7\sqrt{65}}{65}$.
故答案為$\frac{7\sqrt{65}}{65}$.
點評 本題考查的是軸對稱-最短路線問題、相似三角形的判定與性質、銳角三角函數等知識,解題的關鍵是學會利用對稱解決最短問題,學會添加常用輔助線,構造直角三角形解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
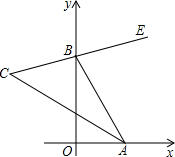 如圖,在直角坐標系中,點A、B分別在射線OX、OY上移動,BE是∠ABY的角平分線,BE的反向延長線與∠OAB的平分線相交于點C,試問∠ACB的大小是否發生變化?如果保持不變,請給出證明.
如圖,在直角坐標系中,點A、B分別在射線OX、OY上移動,BE是∠ABY的角平分線,BE的反向延長線與∠OAB的平分線相交于點C,試問∠ACB的大小是否發生變化?如果保持不變,請給出證明.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
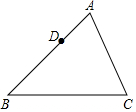 如圖,已知銳角△ABC,點D是AB邊上的一定點,請用尺規在AC邊上求作一點E,使△ADE與△ABC相似.(作出符合題意的一個點即可,保留作圖痕跡,不寫作法.)
如圖,已知銳角△ABC,點D是AB邊上的一定點,請用尺規在AC邊上求作一點E,使△ADE與△ABC相似.(作出符合題意的一個點即可,保留作圖痕跡,不寫作法.)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 二次函數y=ax2+bx+c的圖象是過點A(-1,-$\frac{5}{2}$),B(0,-4),C(4,0)的一條拋物線.
二次函數y=ax2+bx+c的圖象是過點A(-1,-$\frac{5}{2}$),B(0,-4),C(4,0)的一條拋物線.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com