
分析 (1)根據(jù)一元二次方程的解法解答即可;
(2)根據(jù)配方法解一元二次方程即可;
(3)根據(jù)二次根式的混合計算解答即可;
(4)根據(jù)二次根式的混合計算解答即可;
(5)根據(jù)二次根式的混合計算解答即可;
(6)根據(jù)三角函數(shù)進行解答即可.
解答 解:①(2x+1)(2x+1-2)=0,
2x+1=0或2x-1=0,
${x_1}=-\frac{1}{2}$,${x_2}=\frac{1}{2}$;
②(x-3)2=16
x-3=±4
x1=7,x2=-1;
③原式=$\frac{1}{4}\sqrt{2}-4\sqrt{3}-\frac{1}{2}\sqrt{2}+\frac{2}{3}\sqrt{3}+4\sqrt{2}$
=($\frac{1}{4}-\frac{1}{2}+4$)$\sqrt{2}$+(-4+$\frac{2}{3}$)$\sqrt{3}$
=$\frac{15}{4}\sqrt{2}-\frac{10}{3}\sqrt{3}$;
④原式=2$ab\sqrt{3a}-\frac{3ab}{2}\sqrt{3a}+ab\sqrt{3a}$
=(2-$\frac{3}{2}+1$)$ab\sqrt{3a}$
=$\frac{3}{2}ab\sqrt{3a}$;
⑤原式=${(\sqrt{5})^2}-{(\sqrt{3}-\sqrt{2})^2}$
=5-(3-2$\sqrt{6}$+2)
=5-3+2$\sqrt{6}$-2
=2$\sqrt{6}$;
⑥原式=$\sqrt{3}$+4×($\frac{{\sqrt{2}}}{2}$)2-2×$\frac{{\sqrt{3}}}{2}$
=$\sqrt{3}+2-\sqrt{3}$
=2.
點評 此題考查實數(shù)的混合計算,關(guān)鍵是根據(jù)一元二次方程、二次根式和三角函數(shù)進行解答.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 30% | B. | 25% | C. | 20% | D. | 15% |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2016-2017學(xué)年江蘇省八年級下學(xué)期第一次月考數(shù)學(xué)試卷(解析版) 題型:選擇題
如圖,四邊形ABCD是平行四邊形,BE平分∠ABC,CF平分∠BCD,BE、CF交于點G.若使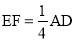 ,那么平行四邊形ABCD應(yīng)滿足的條件是【 】
,那么平行四邊形ABCD應(yīng)滿足的條件是【 】
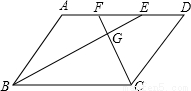
A.∠ABC=60° B.AB:BC=1:4 C.AB:BC=5:2 D.AB:BC=5:8
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2016-2017學(xué)年江蘇省八年級下學(xué)期第一次月考數(shù)學(xué)試卷(解析版) 題型:單選題
如圖,將△ABC繞著點C順時針旋轉(zhuǎn)45°后得到△A′B′C.若∠A=45°.∠B′=110°,則∠BCA′的度數(shù)是( )
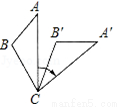
A. 30° B. 70° C. 80° D. 110°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 點P在⊙O內(nèi) | B. | 點P在⊙O上 | C. | 點P在⊙O外 | D. | 無法確定 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
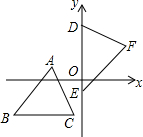 如圖,坐標(biāo)平面上,△ABC≌△FDE,若A點的坐標(biāo)為(a,1),BC∥x軸,B點的坐標(biāo)為(b,-3),D、E兩點在y軸上,則F點到y(tǒng)軸的距離為4.
如圖,坐標(biāo)平面上,△ABC≌△FDE,若A點的坐標(biāo)為(a,1),BC∥x軸,B點的坐標(biāo)為(b,-3),D、E兩點在y軸上,則F點到y(tǒng)軸的距離為4.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
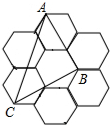 如圖,由7個形狀、大小完全相同的正六邊形組成的網(wǎng)格,正六邊形的頂點稱為格點,已知每個正六邊形的邊長為1,△ABC的頂點都在格點上,則△ABC的面積是( )
如圖,由7個形狀、大小完全相同的正六邊形組成的網(wǎng)格,正六邊形的頂點稱為格點,已知每個正六邊形的邊長為1,△ABC的頂點都在格點上,則△ABC的面積是( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com