
 如圖,已知線段AB,分別以A、B為圓心,大于$\frac{1}{2}$AB長為半徑畫弧,兩弧相交于點C、Q,連接CQ與AB相交于點D,連接AC,BC,E為AC的中點,連接DE,當線段AB=4,∠ACB=60°時,△CED周長是2$\sqrt{3}$+4.
如圖,已知線段AB,分別以A、B為圓心,大于$\frac{1}{2}$AB長為半徑畫弧,兩弧相交于點C、Q,連接CQ與AB相交于點D,連接AC,BC,E為AC的中點,連接DE,當線段AB=4,∠ACB=60°時,△CED周長是2$\sqrt{3}$+4. 分析 由作圖的過程可知CQ是線段AB的垂直平分線,所以可得D為AB中點,結合已知條件可得DE是△ABC的中位線,所以DE的長可求出,再由勾股定理可求出CD的長,由E是AC的中點可求出CE的長,進而可求出△CED的周長.
解答 解:
∵分別以A、B為圓心,大于$\frac{1}{2}$AB長為半徑畫弧,兩弧相交于點C、Q,連接CQ與AB相交于點D,
∴CQ是線段AB的垂直平分線,
∴CA=CB,
∵∠ACB=60°,
∴△ACB是等邊三角形,
∴AC=AB=BC=4,
∴CD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵E為AC的中點,D是AB中點,
∴DE是△ABC的中位線,
∴DE=$\frac{1}{2}$BC=2,
∴△CED周長=2+2+2$\sqrt{3}$=4+2$\sqrt{3}$.
故答案為:4+2$\sqrt{3}$.
點評 本題考查了基本作圖中作已知線段的垂直平分線及線段的垂直平分線的性質,能夠判定△ACB是等邊三角形是解題的關鍵,題目難度不大.


 高中必刷題系列答案
高中必刷題系列答案科目:初中數學 來源: 題型:解答題
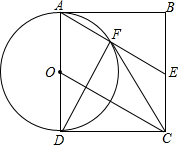 如圖,四邊形ABCD為矩形,E為BC邊中點,以AD為直徑的⊙O與AE交于點F.
如圖,四邊形ABCD為矩形,E為BC邊中點,以AD為直徑的⊙O與AE交于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com