
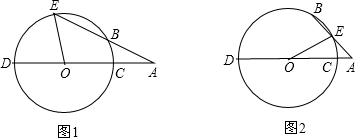
分析 (1)連接OB,則OB=OC,根據等邊對等角得出∠1=∠A,∠2=∠E,進而根據三角形外角的性質求得∠E=2∠A,得出∠DOE=∠E+∠A=3∠A;
(2)連接OB,則OB=OC,根據等邊對等角得出∠AOB=∠A,∠OBE=∠OEB,進而根據三角形內角和定理求得即可求得∴∠DOE=∠BOD+∠BOE=180°-∠AOB+∠BOE=180°-∠A+4∠A-180°=3∠A.
解答 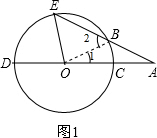 解:(1)∠DOE=3∠A;
解:(1)∠DOE=3∠A;
連接OB,則OB=OC,
∵AB=OC.
∴OB=AB,
∴∠1=∠A,
∵OE=OB,
∴∠2=∠E,
∵∠2=∠1+∠A=2∠A,
∴∠E=2∠A,
∴∠DOE=∠E+∠A=3∠A;
(2)成立;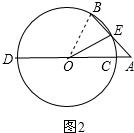
連接OB,則OB=OC,
∵AB=OC.
∴OB=AB,
∴∠AOB=∠A,
∴∠B=180°-2∠A,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠BOE=180°-2∠B=180°-2(180°-2∠A)=4∠A-180°,
∴∠DOE=∠BOD+∠BOE=180°-∠AOB+∠BOE=180°-∠A+4∠A-180°=3∠A.
點評 本題考查了等腰三角形的性質,三角形外角的性質以及三角形內角和定理,熟練掌握性質定理是解題的關鍵.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:解答題
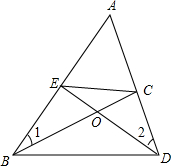 如圖,△ABD中,點E、C分別在AB、AD上,BC與DE相交于點O,若∠1=∠2.求證:
如圖,△ABD中,點E、C分別在AB、AD上,BC與DE相交于點O,若∠1=∠2.求證:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,E是四邊形ADBC內的一點,連接AE,CE,DE,AB,如果$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$,△ADB與△AEC相似嗎?為什么?
如圖,E是四邊形ADBC內的一點,連接AE,CE,DE,AB,如果$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$,△ADB與△AEC相似嗎?為什么?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (a-b)(-a+b) | B. | (m3-n3)(m3+n3) | C. | (-7-x)(7-x) | D. | (x2-y2)(y2+x2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com