
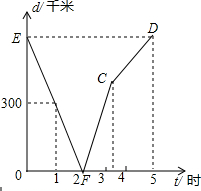
 甲、乙兩列火車分別從A,B兩城同時相向勻速駛出,甲車開往終點B城,乙車開往終點A城,乙車比甲車早到達終點;如圖,是兩車相距的路程d(千米)與行駛時間t(小時)的函數關系圖象.
甲、乙兩列火車分別從A,B兩城同時相向勻速駛出,甲車開往終點B城,乙車開往終點A城,乙車比甲車早到達終點;如圖,是兩車相距的路程d(千米)與行駛時間t(小時)的函數關系圖象.分析 (1)觀察函數圖象,發現當d=0時,t=2,即2小時兩車相遇;
(2)由函數圖象可知甲車5小時到達B城,根據“速度=路程÷時間”即可求出甲車的速度,再根據兩車2小時相遇可算出兩車的速度和,用兩車速度和減去甲車速度即可得出乙車的速度;
(3)由甲車從A城出發,結合“距離=甲車速度×時間”即可得出s甲關于x的函數解析式;由乙車從B城出發,結合“距離=兩地距離-乙車速度×時間”即可得出s乙關于x的函數解析式;
(4)根據“行駛時間=兩車行駛的路程÷兩車的速度和”結合兩車行駛的過程,即可得出結論.
解答 解:(1)觀察函數圖象可以發現:
當t=1時,d=300,而t=2時,d=0,
∴當t=0時,d=2×(300-0)=600.
∴A、B兩地相距600千米.
當d=0時,t=2,
∴經過2小時兩車相遇.
故答案為:600,2.
(2)甲車的速度為:600÷5=120(千米/時);
乙車的速度為:600÷2-120=180(千米/時).
答:甲車的速度為120千米/時,乙車的速度為180千米/時.
(3)結合題意可知:s甲=120x,
s乙=600-180x.
(4)兩車第一次相距100千米的時間為:(600-100)÷(180+120)=$\frac{5}{3}$(小時);
兩車第二次相距100千米的時間為:(600+100)÷(180+120)=$\frac{7}{3}$(小時).
∵180×$\frac{7}{3}$=420(千米),420<600,
∴第二次相距100千米時,乙車尚未到達終點,該時間符合題意.
答:當兩車相距100千米路程時,t的值為$\frac{5}{3}$小時或$\frac{7}{3}$小時.
點評 本題考查了一次函數的應用以及一次函數的圖象,屬于基礎題,難度不大,解決該題型題目時,根據數量關系列出算式(或函數關系式)是關鍵.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:選擇題
| A. | 3-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | -3-$\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -t2的系數是-1 | B. | -$\frac{2mn}{3}$的系數是-$\frac{2}{3}$ | ||
| C. | xy2的系數是1 | D. | 3πa2的系數是3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com