
| 甲種 食物 | 乙種 食物 | 丙種 食物 | 每千克生產(chǎn)成本(元) | |||
| 甲種食物 | 9 | |||||
| 維生素A(單位/千克) | 400 | 600 | 400 | 乙種食物 | 12 | |
| 維生素B(單位/千克) | 800 | 200 | 400 | 丙種食物 | 8 |
分析 (1)根據(jù)“甲、乙、丙三種食物混合研制成100千克食物,混合食品中至少需含44000單位的維生素A和48000單位的維生素B”列出等式或不等式$\left\{\begin{array}{l}{x+y+z=100}\\{400x+600y+400z≥44000}\\{800x+200y+400z≥48000}\end{array}\right.$,整理并解不等式,可得y≥20且2x-y≥40;
(2)①根據(jù)“總成本=甲種食物的質(zhì)量×每千克生產(chǎn)成本+乙種食物的質(zhì)量×每千克生產(chǎn)成本+丙種食物的質(zhì)量×每千克生產(chǎn)成本”可得P關(guān)于x、y的代數(shù)式;②由x=40、y≥20且2x-y≥40得20≤y≤40,根據(jù)P=x+4y+800=4y+840中P隨y的增大而增大,從而得出w的取值范圍及最小值,繼而可得乙、丙兩種食物的質(zhì)量.
解答 解:(1)根據(jù)題意得:
$\left\{\begin{array}{l}{x+y+z=100}\\{400x+600y+400z≥44000}\\{800x+200y+400z≥48000}\end{array}\right.$,
整理得$\left\{\begin{array}{l}{x+y+z=100}\\{2x+3y+2z≥220}\\{4x+y+2z≥240}\end{array}\right.$,
由x+y+z=100得,z=100-x-y ①
把①代入兩個(gè)不等式可得y≥20且2x-y≥40;
(2)①P=9x+12y+8(100-x-y)=x+4y+800;
②∵x=40,y≥20且2x-y≥40,
∴20≤y≤40,
由題意可得P=x+4y+800=4y+840,
∵P隨y的增大而增大,
∴當(dāng)y=20,z=40時(shí),P有最小值40×9+12×20+8×40=920元;
當(dāng)y=40,z=20時(shí),P有最大值40×9+12×40+8×20=1000元;
則P的取值范圍是920≤P≤1000.
P取最小值時(shí),乙、丙兩種食物的質(zhì)量分別是20千克、40千克.
點(diǎn)評(píng) 本題考查一元一次不等式組的應(yīng)用、一次函數(shù)的應(yīng)用,理清題中所涉數(shù)量關(guān)系,根據(jù)相等關(guān)系或不等關(guān)系列出不等式關(guān)系式即可求解,P的取值需要分組討論得出.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
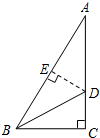 如圖,在Rt△ABC中,∠C=90°,∠ABC的平分線BD交AC于D,若CD=3cm,則點(diǎn)D到AB的距離DE是( )
如圖,在Rt△ABC中,∠C=90°,∠ABC的平分線BD交AC于D,若CD=3cm,則點(diǎn)D到AB的距離DE是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
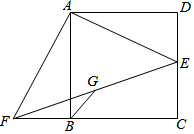 E為正方形ABCD的邊CD上的一點(diǎn),將△ADE繞A點(diǎn)順時(shí)針旋轉(zhuǎn)90°,得△ABF,G為EF中點(diǎn).下列結(jié)論:
E為正方形ABCD的邊CD上的一點(diǎn),將△ADE繞A點(diǎn)順時(shí)針旋轉(zhuǎn)90°,得△ABF,G為EF中點(diǎn).下列結(jié)論:查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com