
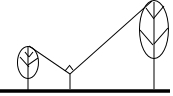
 如圖,身高1.5米的人站在兩棵樹之間,距較高的樹5米,距較矮的樹3米,若此人觀察的樹梢所成的視線的夾角是90°,且較矮的樹高4米,那么較高的樹有多少米?
如圖,身高1.5米的人站在兩棵樹之間,距較高的樹5米,距較矮的樹3米,若此人觀察的樹梢所成的視線的夾角是90°,且較矮的樹高4米,那么較高的樹有多少米? 分析 過點E作EH⊥AB,EM⊥CD,H、M為垂足,根據相似三角形的判定定理得出△AHE∽△EMC,由相似三角形的對應邊成比例求出CM的長,進而可得出結論.
解答 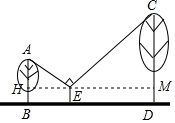 解:過點E作EH⊥AB,EM⊥CD,H、M為垂足,則∠A+∠AEH=90°.
解:過點E作EH⊥AB,EM⊥CD,H、M為垂足,則∠A+∠AEH=90°.
∵∠AEC=90°,
∴∠AEH+∠CEM=90°,
∴∠A=∠CEM.
∵∠AHE=∠CME=90°,
∴△AHE∽△EMC,
∴$\frac{AH}{EM}$=$\frac{HE}{CM}$,即$\frac{4-1.5}{5}$=$\frac{3}{CM}$,解得CM=6,
∴CD=CM+DM=6+1.5=7.5(米).
點評 本題考查的是相似三角形的應用,根據題意作出輔助線,構造出相似三角形是解答此題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
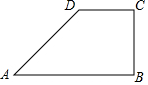 如圖,四邊形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.
如圖,四邊形ABCD中,AB||CD,BC⊥AB;AD=5,CD=3,BC=4.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
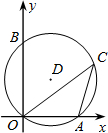 如圖,點O為坐標原點,點A的坐標為(3,0),點B的坐標為(0,4),⊙D過A,B,O三點,點C為$\widehat{OBA}$上的一點(不與O、A兩點重合),連接OC,AC,則cosC的值為( )
如圖,點O為坐標原點,點A的坐標為(3,0),點B的坐標為(0,4),⊙D過A,B,O三點,點C為$\widehat{OBA}$上的一點(不與O、A兩點重合),連接OC,AC,則cosC的值為( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ①② | B. | ②④ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com