下列代數式中，單項式共有（ ）
a， －2ab，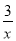 
， 
， 
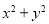， －1， 
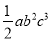
A．3個 B．4個 C．5個 D．6個
科目：初中數學 來源：2014-2015學年江蘇省江陰市要塞片八年級上學期期中考試數學試卷（解析版） 題型：選擇題
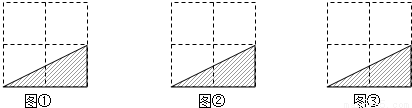
（本題滿分6分）請在下列三個2×2的方格中，各畫出一個三角形，要求所畫三角形是圖中三角形經過軸對稱變換后得到的圖形，且所畫的三角形頂點與方格中的小正方形頂點重合，并將所畫三角形涂上陰影．（注：所畫的三個圖形不能重復）
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市要塞片九年級上學期期中考試數學試卷（解析版） 題型：選擇題
為了調查某小區居民的用水情況，隨機抽查了若干戶家庭的月用水量，結果如下表：
月用水量（噸） | 3 | 4 | 5 | 8 |
戶 數 | 2 | 3 | 4 | 1 |
則關于這若干戶家庭的月用水量，下列說法錯誤的是（ ）
A．平均數是4.6 B．中位數是4
C．眾數是5 D．調查了10戶家庭的月用水量
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市要塞片七年級上學期期中考試數學試卷（解析版） 題型：填空題
若代數式x2+3x－5的值為2，則代數式－2x2－6x+3的值為 ．
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市八年級上學期期中考試數學試卷（解析版） 題型：解答題
（本題6分）如圖1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小敏將一塊三角板中含45°角的頂點放在A上，從AB邊開始繞點A逆時針旋轉一個角α，其中三角板斜邊所在的直線交直線BC于點D，直角邊所在的直線交直線BC于點E．
（1）小敏在線段BC上取一點M，連接AM，旋轉中發現：若AD平分∠BAM，則AE也平分∠MAC．請你證明小敏發現的結論；
（2）當0°＜α≤45°時，小敏在旋轉中還發現線段BD、CE、DE之間存在如下等量關系：BD2+CE2=DE2．同組的小穎和小亮隨后想出了兩種不同的方法進行解決；小穎的想法：將△ABD沿AD所在的直線對折得到△ADF（如圖2）；小亮的想法：將△ABD繞點A順時針旋轉90°得到△ACG（如圖3）．請你選擇其中的一種方法證明小敏的發現的是正確的．
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市八年級上學期期中考試數學試卷（解析版） 題型：填空題
把三邊分別為BC＝3，AC＝4，AB＝5的三角形沿最長邊AB翻折成
△ABC'，則CC'的長為
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省江陰市九年級上學期期中考試數學試卷（解析版） 題型：解答題
閱讀材料：（8分）
例：說明代數式 
的幾何意義，并求它的最小值．
【解析】
，如圖，建立平面直角坐標系，點P（x，0）是x軸上一點，則
可以看成點P與點A（0，1）的距離，
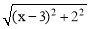可以看成點P與點B（3，2）的距離，所以原代數式的值可以看成線段PA與PB長度之和，它的最小值就是PA＋PB的最小值．
設點A關于x軸的對稱點為A′，則PA＝PA′，因此，求PA＋PB的最小值，只需求PA′＋PB的最小值，而點A′、B間的直線段距離最短，所以PA′＋PB的最小值為線段A′B的長度．為此，構造直角三角形A′CB，因為A′C＝3，CB＝3，所以A′B＝3
， 即原式的最小值為3．
根據以上閱讀材料，解答下列問題：
（1）代數式
的值可以看成平面直角坐標系中點P（x，0）與點A（1，1）、點B 的距離之和．（填寫點B的坐標）
（2）代數式 
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
