
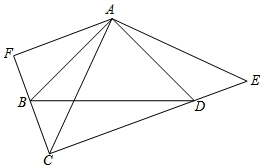
 如圖,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足為F.
如圖,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足為F.分析 (1)根據兩邊夾角對應相等的兩個三角形全等,即可證明.
(2)想辦法證明∠ACB=∠ACE=45°即可解決問題.
(3)結論:CE=2AF.過點A作AG⊥CG,垂足為點G.先證明AF=AG,再證明CE=2AG即可.
解答 (1)證明:∵∠BAD=∠CAE=90°,
∴∠BAD-∠CAD=∠CAE-∠CAD,
∴∠BAC=∠EAD,
在△ABC和△ADE中
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AC=AE}\end{array}\right.$,
∴△ABC≌△ADE(SAS).
(2)證明:∵∠CAE=90°,AC=AE
∴∠ACE=∠AEC=45°
∵△ABC≌△ADE
∴∠ACB=∠AEC=45°
∴∠ACB=∠ACE
∴AC平分∠ECF 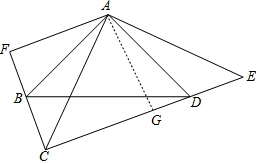
(3)解:結論:CE=2AF.
理由:過點A作AG⊥CG,垂足為點G
∵AC平分∠ECF,AF⊥CB,AG⊥CG,
∴AF=AG,
又∵AC=AE,AG⊥CG,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC=45°,
∴CG=AG=GE,
∴CE=2AG,
∴CE=2AF.
點評 本題考查全等三角形的判定和性質、等腰直角三角形的性質、角平分線的性質定理等知識,解題的關鍵是熟練掌握全等三角形的判定和性質,學會添加常用輔助線,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
 如圖,射線AB∥射線CD,∠CAB與∠ACD的平分線交于點E,AC=4,點P是射線AB上的一動點,連結PE并延長交射線CD于點Q.給出下列結論:①△ACE是直角三角形;②S四邊形APQC=2S△ACE;③設AP=x,CQ=y,則y關于x的函數表達式是y=-x+4(0≤x≤4),其中正確的是( )
如圖,射線AB∥射線CD,∠CAB與∠ACD的平分線交于點E,AC=4,點P是射線AB上的一動點,連結PE并延長交射線CD于點Q.給出下列結論:①△ACE是直角三角形;②S四邊形APQC=2S△ACE;③設AP=x,CQ=y,則y關于x的函數表達式是y=-x+4(0≤x≤4),其中正確的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | 14 | B. | 7 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
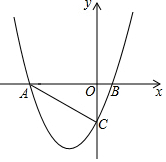 如圖,拋物線y=ax2+bx+c交x軸于A(-4,0),B(1,0),交y軸于C點,且OC=2OB.
如圖,拋物線y=ax2+bx+c交x軸于A(-4,0),B(1,0),交y軸于C點,且OC=2OB.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com