
分析 (1)根據(jù)方程的系數(shù)結(jié)合根的判別式即可得出△>0,此題得證;
(2)根據(jù)根與系數(shù)的關(guān)系即可得出x1+x2=-a、x1•x2=a-2,結(jié)合$|{x_1}-{x_2}|=\sqrt{13}$即可得出關(guān)于a的一元二次方程,解之即可得出a的值.
解答 (1)證明:在方程x2+ax+a-2=0中,△=a2-4(a-2)=(a-2)2+4,
∵(a-2)2≥0,
∴△>0,
故不論a為何實(shí)數(shù),此方程總有兩個(gè)不相等的實(shí)數(shù)根.
(2)解:∵方程x2+ax+a-2=0的兩個(gè)實(shí)數(shù)根分別為x1,x2,
∴x1+x2=-a,x1•x2=a-2,
∵$|{x_1}-{x_2}|=\sqrt{13}$,
∴${({x_1}-{x_2})^2}=13$,
∴${({x_1}+{x_2})^2}-4{x_1}{x_2}=13$,即a2-4(a-2)=13,
整理得:(a-2)2=9,
解得:a1=5,a2=-1.
點(diǎn)評(píng) 本題考查了根的判別式以及根與系數(shù)的關(guān)系,熟練掌握“當(dāng)△>0時(shí),方程有兩個(gè)不相等的兩個(gè)實(shí)數(shù)根”是解題的關(guān)鍵.


 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
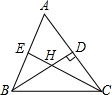 如圖,在△ABC中,高BD,CE相交于H,已知∠HBC-∠HCB=10°,∠ABD=$\frac{1}{2}$∠HBC,求∠A的度數(shù).
如圖,在△ABC中,高BD,CE相交于H,已知∠HBC-∠HCB=10°,∠ABD=$\frac{1}{2}$∠HBC,求∠A的度數(shù).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 在平面直角坐標(biāo)系xOy中,將拋物線y=2x2沿y軸向上平移1個(gè)單位,再沿x軸向右平移2個(gè)單位,平移后拋物線的頂點(diǎn)坐標(biāo)記作A,直線x=3與平移后的拋物線相交于B,與直線OA相交于C.
在平面直角坐標(biāo)系xOy中,將拋物線y=2x2沿y軸向上平移1個(gè)單位,再沿x軸向右平移2個(gè)單位,平移后拋物線的頂點(diǎn)坐標(biāo)記作A,直線x=3與平移后的拋物線相交于B,與直線OA相交于C.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
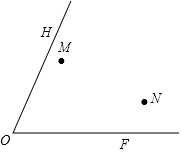 現(xiàn)有M和N兩個(gè)村莊,欲在其旁兩條公路OH、OF上建立A、B兩個(gè)候車廳,使MA+AB+BN距離最小,請(qǐng)你在OH、OF上確定A、B兩點(diǎn)的位置(保留作圖痕跡)
現(xiàn)有M和N兩個(gè)村莊,欲在其旁兩條公路OH、OF上建立A、B兩個(gè)候車廳,使MA+AB+BN距離最小,請(qǐng)你在OH、OF上確定A、B兩點(diǎn)的位置(保留作圖痕跡)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com