Question

15．已知∠AOB=α°，過點O作OB⊥OC．請畫圖示意并求解．
（1）若α=30，則∠AOC=60°或120°；
（2）若α=40，射線OE平分∠AOC，射線OF平分∠BOC，求∠EOF的度數；
（3）若0＜α＜180，射線OE平分∠AOC，射線OF平分∠BOC，則∠EOF=$\frac{α}{2}$°．

Answer 1

分析 （1）由OB⊥OC可得出∠BOC=90°，分射線OA、OC在射線OB同側和兩側討論，結合圖形即可得出結論；
（2）分射線OA、OC在射線OB同側和兩側討論，根據角平分線定義即可得出∠COE和∠COF的大小，結合圖形即可求出∠EOF的度數；
（3）分射線OA、OC在射線OB同側和兩側討論，根據角平分線定義即可得出∠COE和∠COF的大小，結合圖形即可求出∠EOF的度數．

解答 解：根據題意畫出圖形，如圖所示．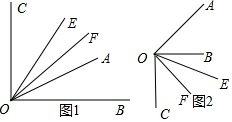
（1）∵OB⊥OC，
∴∠BOC=90°．
當射線OA、OC在射線OB同側時，∠AOC=∠BOC-∠AOB=60°；
當射線OA、OC在射線OB兩側時，∠AOC=∠AOB+∠BOC=120°．
故答案為：60°或120°．
（2）當射線OA、OC在射線OB同側時，
∵射線OE平分∠AOC，射線OF平分∠BOC，
∴∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$（∠BOC-∠AOB）=$\frac{1}{2}$×（90°-40°）=25°，∠COF=$\frac{1}{2}$∠BOC=45°，
∴∠EOF=∠COF-∠COE=45°-25°=20°；
當射線OA、OC在射線OB兩側時，
∵射線OE平分∠AOC，射線OF平分∠BOC，
∴∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$（∠BOC+∠AOB）=$\frac{1}{2}$×（90°+40°）=65°，∠COF=$\frac{1}{2}$∠BOC=45°，
∴∠EOF=∠COE-∠COF=65°-45°=20°．
綜上可知：∠EOF的度數為20°．
（3）當射線OA、OC在射線OB同側時，
∵射線OE平分∠AOC，射線OF平分∠BOC，
∴∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$（∠BOC-∠AOB）=$\frac{1}{2}$×（90°-α°）=45°-$\frac{α}{2}$°，∠COF=$\frac{1}{2}$∠BOC=45°，
∴∠EOF=∠COF-∠COE=45°-（45°-$\frac{α}{2}$°）=$\frac{α}{2}$°；
當射線OA、OC在射線OB兩側時，
∵射線OE平分∠AOC，射線OF平分∠BOC，
∴∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$（∠BOC+∠AOB）=$\frac{1}{2}$×（90°+α°）=45°+$\frac{α}{2}$°，∠COF=$\frac{1}{2}$∠BOC=45°，
∴∠EOF=∠COE-∠COF=（45°+$\frac{α}{2}$°）-45°=$\frac{α}{2}$°．
故答案為：$\frac{α}{2}$°．

點評 本題考查了垂直、角平分線的定義以及角的計算，依照題意畫出圖形利用數形結合解決問題是解題的關鍵．