
 如圖,⊙A的圓心A在反比例函數(shù)y=$\frac{3}{x}$(x>0)的圖象上,且與x軸、y軸相切于點(diǎn)B、C,一次函數(shù)y=$\frac{{\sqrt{3}}}{3}$x+b的圖象經(jīng)過點(diǎn)C,且與x軸交于點(diǎn)D,與⊙A的另一個(gè)交點(diǎn)為點(diǎn)E.
如圖,⊙A的圓心A在反比例函數(shù)y=$\frac{3}{x}$(x>0)的圖象上,且與x軸、y軸相切于點(diǎn)B、C,一次函數(shù)y=$\frac{{\sqrt{3}}}{3}$x+b的圖象經(jīng)過點(diǎn)C,且與x軸交于點(diǎn)D,與⊙A的另一個(gè)交點(diǎn)為點(diǎn)E.分析 (1)如圖1中,連接AC、AB.首先證明四邊形ABOC是正方形,求出點(diǎn)C坐標(biāo),利用待定系數(shù)法即可解決問題.
(2)如圖2中,連接BC、BE,作AM⊥CE于M.在Rt△DOC中,由tan∠CDO=$\frac{OC}{DO}$=$\frac{\sqrt{3}}{3}$,推出∠CDO=30°,由AC∥BD,推出∠ECA=∠CDO=30°,∠CAM=60°,
由AM⊥CE,推出∠CAM=∠EAM=60°,推出∠CAE=120°,在Rt△AMC中,根據(jù)CM=AC•cos30°=$\frac{3}{2}$,推出CE=2CM=3,可得∠CBE=$\frac{1}{2}$∠CAE=60°,由此即可解決問題.
(3)分兩種情形求解如圖3中,當(dāng)⊙A″與直線y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$相切于點(diǎn)E,AB與直線CD交于點(diǎn)K,想辦法求出AA″,即可解決問題.同法求出AA′.
解答 解:(1)如圖1中,連接AC、AB.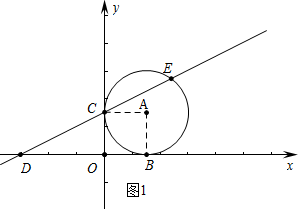
∵⊙A與x軸、y軸相切于點(diǎn)B、C,
∴AC⊥OC,AB⊥OB,AC=AB,四邊形ABOC是正方形,設(shè)A(m,m),
∵點(diǎn)A在y=$\frac{3}{x}$上,
∴m2=3,
∵m>0,
∴點(diǎn)A坐標(biāo)($\sqrt{3}$,$\sqrt{3}$),
∴OC=$\sqrt{3}$,
∴點(diǎn)C坐標(biāo)(0,$\sqrt{3}$),
∵一次函數(shù)y=$\frac{{\sqrt{3}}}{3}$x+b的圖象經(jīng)過點(diǎn)C,
∴b=$\sqrt{3}$,
∴一次函數(shù)的解析式為y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,令y=0得x=-3,
∴D(-3,0),b=$\sqrt{3}$.
(2)如圖2中,連接BC、BE,作AM⊥CE于M.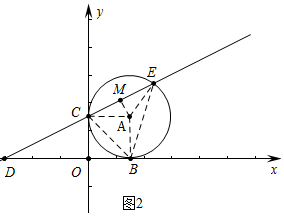
在Rt△DOC中,∵tan∠CDO=$\frac{OC}{DO}$=$\frac{\sqrt{3}}{3}$,
∴∠CDO=30°,
∵AC∥BD,
∴∠ECA=∠CDO=30°,∠CAM=60°,
∵AM⊥CE,
∴∠CAM=∠EAM=60°,
∴∠CAE=120°,
在Rt△AMC中,CM=AC•cos30°=$\frac{3}{2}$,
∴CE=2CM=3,
∴∠CBE=$\frac{1}{2}$∠CAE=60°.
(3)如圖3中,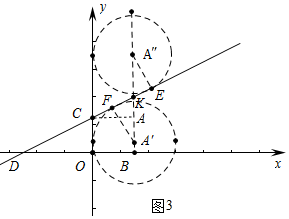
①當(dāng)⊙A″與直線y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$相切于點(diǎn)E,AB與直線CD交于點(diǎn)K,
∵AB∥OC,
∴∠A″KE=∠DKB=∠DCO=60°,
在Rt△A″EK中,A″E=$\sqrt{3}$,A″K=A″E•cos30°=$\frac{3}{2}$,
在Rt△CKA中,AK=CA•tan30°=1,
∴AA″=A″K+AK=1+$\frac{3}{2}$=$\frac{5}{2}$,
∴⊙A向上平移$\frac{5}{2}$的單位⊙A與y軸及直線y=$\frac{{\sqrt{3}}}{3}$x+$\sqrt{3}$均相切.
②同理可得⊙A向下平移$\frac{1}{2}$個(gè)單位⊙A與y軸及直線y=$\frac{{\sqrt{3}}}{3}$x+$\sqrt{3}$均相切.
點(diǎn)評 本題考查圓綜合題、一次函數(shù)的應(yīng)用、反比例函數(shù)的應(yīng)用、銳角三角函數(shù)、正方形的性質(zhì)等知識,解題的關(guān)鍵是靈活運(yùn)用所學(xué)知識解決問題,學(xué)會(huì)添加常用輔助線,構(gòu)造特殊三角形解決問題,屬于中考常考題型.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 6.96×103 | B. | 69.6×105 | C. | 6.96×105 | D. | -6.96×105 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a=5 | B. | a≥5 | C. | a=3 | D. | a≥3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3cm,3cm,4cm | B. | 7cm,4cm,2cm | C. | 3cm,4cm,8cm | D. | 2cm,3cm,5cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
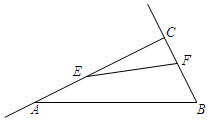 如圖,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,點(diǎn)E從點(diǎn)C出發(fā)沿射線CA以每秒2cm的速度運(yùn)動(dòng),同時(shí)點(diǎn)F從點(diǎn)B出發(fā)沿射線BC以每秒1
如圖,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,點(diǎn)E從點(diǎn)C出發(fā)沿射線CA以每秒2cm的速度運(yùn)動(dòng),同時(shí)點(diǎn)F從點(diǎn)B出發(fā)沿射線BC以每秒1查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,兩張寬度相等的紙條疊放在一起,重疊部分構(gòu)成四邊形ABCD.
如圖,兩張寬度相等的紙條疊放在一起,重疊部分構(gòu)成四邊形ABCD.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com