
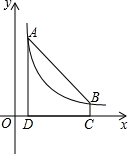
 如圖,點A(1,6)和點B在反比例函數圖象上,AD⊥x軸于點D,BC⊥x軸于點C,DC=5.
如圖,點A(1,6)和點B在反比例函數圖象上,AD⊥x軸于點D,BC⊥x軸于點C,DC=5.分析 (1)根據待定系數法即可求得反比例函數的解析式組,進而確定出B橫坐標坐標,橫坐標代入即可確定出縱坐標;
(2)存在,設E(x,0),表示出DE與CE,連接AE,BE,三角形ABE面積=四邊形ABCD面積-三角形ADE面積-三角形BCE面積,求出即可.
解答 解:(1)∵點A(1,6)和點B在反比例函數圖象上,
∴k=1×6=6,
∴反比例函數的表達式為:y=$\frac{6}{x}$;
∵AD⊥x軸于點D,
∴D(1,0),
∵BC⊥x軸于點C,DC=5.
∴B的橫坐標為6,
將x=6代入y=$\frac{6}{x}$解得,y=1,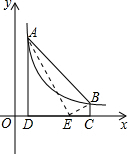
∴B(6,1).
(2)存在,
設E(x,0),則DE=x-1,CE=6-x,
∵AD⊥x軸,BC⊥x軸,
∴∠ADE=∠BCE=90°,
連接AE,BE,
則S△ABE=S四邊形ABCD-S△ADE-S△BCE
=$\frac{1}{2}$(BC+AD)•DC-$\frac{1}{2}$DE•AD-$\frac{1}{2}$CE•BC
=$\frac{1}{2}$×(1+6)×5-$\frac{1}{2}$(x-1)×6-$\frac{1}{2}$(6-x)×1
=$\frac{35}{2}$-$\frac{5}{2}$x=5,
解得:x=5,
則E(5,0).
點評 此題考查了待定系數法求反比例函數解析式,反比例函數圖象上點的坐標特征以及三角形、梯形的面積等,熟練掌握待定系數法是解本題的關鍵.


科目:初中數學 來源: 題型:選擇題
 如圖,某水庫堤壩橫斷面迎水坡AB的斜面坡度是1:$\sqrt{3}$,堤壩高BC=50m,則迎水坡面AB的長度是( )
如圖,某水庫堤壩橫斷面迎水坡AB的斜面坡度是1:$\sqrt{3}$,堤壩高BC=50m,則迎水坡面AB的長度是( )| A. | 100m | B. | 120m | C. | 50$\sqrt{3}$m | D. | 100$\sqrt{3}$m |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
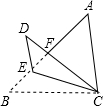 如圖,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.
如圖,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com