把一個底面半徑10厘米的圓錐形金屬鑄件浸沒在一個底面半徑為15厘米的圓柱形容器中,結果水面比原來升高了2厘米,求這個圓錐形鑄件的高.
解:上升2厘米的水的體積是:
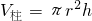
=π×15
2×2=450π(立方厘米),
即金屬鑄件的體積是:V
錐=450π立方厘米,
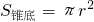
=π×10
2=100π(平方厘米),
所以金屬鑄件的高是:450π×3÷100π=13.5(厘米),
答:這個圓錐形鑄件的高為13.5厘米.
分析:根據題干可知,這個圓錐形金屬鑄件的體積,就等于圓柱形容器內水面上升2厘米高的水的體積,由此先求出這個金屬鑄件的體積,再利用圓錐的高=體積×3÷底面積,即可解答問題.
點評:此題考查了圓柱與圓錐的體積公式的靈活應用,抓住上升部分水的體積求出金屬鑄件的體積是解決本題的關鍵.

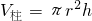 =π×152×2=450π(立方厘米),
=π×152×2=450π(立方厘米),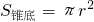 =π×102=100π(平方厘米),
=π×102=100π(平方厘米),
