
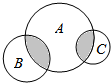
 如圖所示,圓B與圓C的面積之和等于圓A面積的$\frac{4}{5}$,且圖A中的陰影部分面積占圓A面積的$\frac{1}{6}$,圓B的陰影部分面積占圓B面積的$\frac{1}{5}$,圓C的陰影部分面積占圓C面積的$\frac{1}{3}$,求圓A、圓B、圓C的面積之比.
如圖所示,圓B與圓C的面積之和等于圓A面積的$\frac{4}{5}$,且圖A中的陰影部分面積占圓A面積的$\frac{1}{6}$,圓B的陰影部分面積占圓B面積的$\frac{1}{5}$,圓C的陰影部分面積占圓C面積的$\frac{1}{3}$,求圓A、圓B、圓C的面積之比. 分析 根據“⊙B與⊙C面積之和等于⊙A面積的$\frac{4}{5}$,”得出,⊙B的面積+⊙C面積=⊙A面積×$\frac{4}{5}$,再根據“⊙A中陰影部分占⊙A面積的$\frac{1}{6}$,”得出⊙A中陰影部分面積=⊙A面積×$\frac{1}{6}$,根據“⊙B中的陰影部分占⊙B面積的$\frac{1}{5}$,”得出,⊙B中的陰影部分面積=⊙B面積×$\frac{1}{5}$,根據“⊙C中的陰影部分占⊙C面積的$\frac{1}{3}$,”得出⊙C中的陰影部分占面積=⊙C面積×$\frac{1}{3}$,由此得出,$\frac{1}{6}$×⊙A=$\frac{1}{3}$×⊙C面積+⊙B面積×$\frac{1}{5}$,所以⊙B面積=$\frac{3}{4}$×⊙A面積,⊙C面積=$\frac{1}{20}$×⊙A面積,進而求出⊙A,⊙B,⊙C的面積之比.
解答 解:因為,⊙B面積+⊙C面積=⊙A面積×$\frac{4}{5}$,
⊙A中陰影部分面積=⊙A面積×$\frac{1}{6}$,
⊙B中陰影部分面積=⊙B面積×$\frac{1}{5}$,
⊙C中陰影部分占面積=⊙C面積×$\frac{1}{3}$,
$\frac{1}{6}$×⊙A面積=$\frac{1}{3}$×⊙C面積+⊙B面積×$\frac{1}{5}$,
由⊙B面積+⊙C面積=⊙A面積×$\frac{4}{5}$轉化得:
①⊙B面積=⊙A面積×$\frac{4}{5}$-⊙C面積;
②⊙C面積=⊙A面積×$\frac{4}{5}$-⊙B面積;
把①②分別代入下面式子
$\frac{1}{6}$×⊙A面積=$\frac{1}{3}$×⊙C面積+⊙B面積×$\frac{1}{5}$,
可得出:
⊙B面積=$\frac{3}{4}$×⊙A面積,⊙C面積=$\frac{1}{20}$×⊙A面積,
所以⊙A,⊙B,⊙C的面積之比是:1:$\frac{3}{4}$:$\frac{1}{20}$=20:15:1.
答:⊙A,⊙B,⊙C的面積之比是20:15:1.
點評 關鍵是根據題意得出數量⊙A,⊙B,⊙C的面積之間的數量關系式,進而用⊙A面積表示出⊙B,⊙C的面積.


科目:小學數學 來源: 題型:解答題
查看答案和解析>>
科目:小學數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com