Question

4．如圖，已知正方形ABCD的周長是40厘米，DE=6.4厘米，陰影部分的面積是32平方厘米．

Answer 1

分析 如下圖所示：連接BD，由等底等高的三角形的面積相等，可知三角形BCD的面積等于三角形BCF的面積，依據等式的性質，把它們的面積都減去重合部分的三角形BCE的面積，剩下的面積也相等，即三角形BDE的面積等于三角形CEF即陰影部分的面積．由此可知，求陰影部分的面積也就是求三角形BDE的面積，已知正方形的周長，用周長除以4即可得到正方形的邊長，即三角形BDE的底邊DE上的高，再利用三角形的面積公式代入數據即可解決．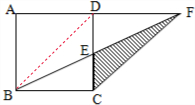

解答 解：由分析可知陰影部分的面積為：
6.4×（40÷4）÷2
=6.4×10÷2
=64÷2
=32（平方厘米）；
答：陰影部分的面積是32平方厘米．
故答案為：32．

點評 本題解決的關鍵是利用轉化的數學思想方法，把求陰影部分的面積轉化為易求面積的三角形的面積，從而利用三角形的面積公式解決問題．