
34.已知函數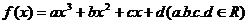 ,且函數
,且函數 的圖像關于原點對稱,其圖像在x=3處的切線方程為8x-y-18=0。
的圖像關于原點對稱,其圖像在x=3處的切線方程為8x-y-18=0。
(1)
求 的解析式;
的解析式;
(2)
是否存在區間[a,b],使得函數g(x)的定義域和值域均為[a,b],且解析式與 的解析式相同?若存在,求出這樣的一個區間[a,b];若不存在,請說明理由。
的解析式相同?若存在,求出這樣的一個區間[a,b];若不存在,請說明理由。
解:(1)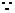
 的圖像關于原點對稱,
的圖像關于原點對稱,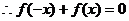 恒成立,即
恒成立,即 恒成立,
恒成立,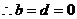 。
。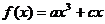 ,
,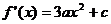
又 的圖像在x=3處的切線方程為
的圖像在x=3處的切線方程為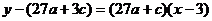 ,
,
即 ,據題意得:
,據題意得: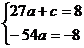 解得:
解得: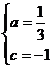 ,
,
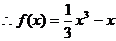
(2)由 得x=0或
得x=0或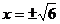 。
。
又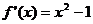 ,由
,由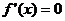 得
得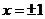 ,且當
,且當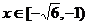 或
或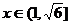 時,
時,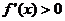 ,當
,當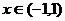 時
時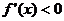 。
。
所以,函數 在
在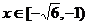 和
和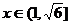 上遞增,在
上遞增,在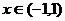 上遞減。
上遞減。
于是,函數在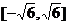 上的極大值和極小值分別為
上的極大值和極小值分別為
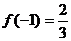 ,
,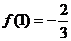 而
而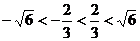 ,
,
故存在這樣的區間[a,b],其中滿足條件的一個區間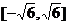
33.曲線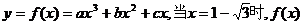 有極小值,當
有極小值,當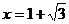 處有極大值,且在x=1處切線的斜率為
處有極大值,且在x=1處切線的斜率為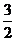 .
.
(1)求 ;
;
(2)曲線上是否存在一點P,使得y= 的圖象關于點P中心對稱?若存在,請求出點P坐標,并給出證明;若不存在,請說明理由.
的圖象關于點P中心對稱?若存在,請求出點P坐標,并給出證明;若不存在,請說明理由.
解:f′(x)=3ax2+2bx+c ∵當x=1± 時 f(x)有極小值及極大值
時 f(x)有極小值及極大值
∴f′(1± )=0 即1±
)=0 即1± 為3ax2+2bx+c=0兩根
為3ax2+2bx+c=0兩根
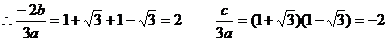
∴b=-3a , c=-6a
又∵f(x)在x=1處切線的斜率為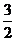
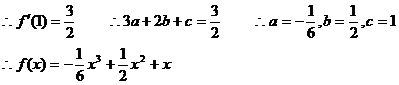
(2)假設存在P(x0, y0),使得f(x)的圖象關于P中心對稱,
則f(x0+x)+f(x0-x)=2y0
即-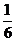 (x0+x)3+
(x0+x)3+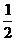 (x0+x)2+x0+x-
(x0+x)2+x0+x-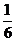 (x0-x)3+
(x0-x)3+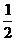 (x0-x)2+x0-x=2y0
(x0-x)2+x0-x=2y0
化解得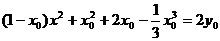
∵對于任意x∈R等式都成立
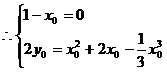
∴x0=1, y0=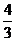 .易知P(1,
.易知P(1,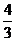 )在曲線y=f(x)上.
)在曲線y=f(x)上.
∴曲線上存在P(1,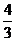 )使得f(x)的圖象關于中心對稱
)使得f(x)的圖象關于中心對稱
32. 如圖,平面PAD
如圖,平面PAD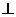 平面ABCD,
平面ABCD, PAD是正三角形,
PAD是正三角形,
ABCD是矩形,M是AB的中點,PC與平面ABCD成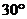 角。
角。
(1)
求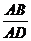 的值;
的值;
(2) 求二面角P-MC-D的大小;
(3) 當AD的長為多少時,點D到平面PMC的距離為2。
解:(1)取AD中點H,則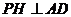 ,
,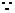 面PAD
面PAD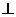 平面ABCD,
平面ABCD,
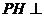 面ABCD,
面ABCD, PC與面ABCD所成的角為
PC與面ABCD所成的角為 。
。
設AD=a,則 ,
, ,
,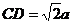

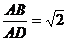 。
。
(2)連結HM,由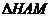 ∽
∽ 可得:
可得: 。
。
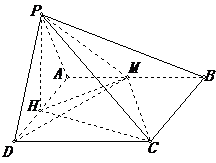
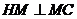 ,由三垂線定理得
,由三垂線定理得 ,
,

 是二面角P-MC-D的平面角。
是二面角P-MC-D的平面角。
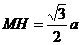 ,
,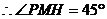 。
。
二面角P-MC-D的平面角為
由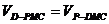 可得:AD=
可得:AD=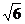 。
。
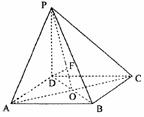
31.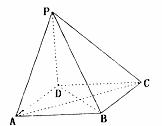 已知ABCD是正方形,PD⊥平面ABCD,PD=AD=2.
已知ABCD是正方形,PD⊥平面ABCD,PD=AD=2.
(Ⅰ)求PC與平面PBD所成的角;
(Ⅱ)求點D到平面PAC的距離;
(Ⅲ)在線段PB上是否存在一點E,使PC⊥平面ADE?
若存在,確定E點的位置,若不存在,說明理由.
解: (Ⅰ)設AC與BD相交于點O,連接PO。
∵ABCD是正方形,∴AC⊥BD。
又∵PD⊥平面ABCD,∴PD⊥AC。
∵BD∩PD=D, ∴AC⊥平面PBD。
∴∠CPO為PC與平面PBD所成的角。
∵PD=AD=2,則OC= ,PC=2
,PC=2 。
。
 在Rt△POC中,∠POC=90°,
在Rt△POC中,∠POC=90°,
∴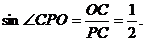
∴PC與平面PBD所成的角為30°
(Ⅱ)過D做DF⊥PO于F,∵AC⊥平面PBD,
DF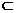 平面PBD, ∴AC⊥DF。
平面PBD, ∴AC⊥DF。
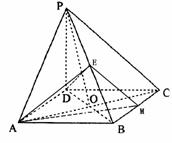 又∵PO∩AC=O,
∴DF⊥平面PAC。
又∵PO∩AC=O,
∴DF⊥平面PAC。
在Rt△PDO中,∠PDO=90°,
∴PO·DF=PD·DO。 ∴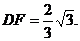
(Ⅲ)假設存在E點,使PC⊥平面ADE.
過E在平面PBC內做EM∥PC交BC于點M,
連接AE、AM.
由AD⊥平面PDC可得AD⊥PC. ∵PC∥EM,∴AD⊥EM.
要使PC⊥平面ADE,即使EM⊥平面ADE. 即使EM⊥AE.
設BM= ,則EM=
,則EM=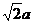 ,EB=
,EB=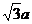 . 在△AEB中由余弦定理得AE2=4+3
. 在△AEB中由余弦定理得AE2=4+3 -4
-4
在Rt△ABM中,∠ABM=90°. ∴AM2=4+ .
.
∵EM⊥AE,∴4+ =4+3
=4+3 -4
-4 +2
+2 . ∴
. ∴ -
- =0. ∵
=0. ∵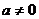 ,∴
,∴ =1.
=1.
∴E為PB的中點,即E為PB的中點時,PC⊥平面ADE.
30.某食品廠定期購買面粉,已知該廠每天需要面粉6噸,每噸面粉的價格為1800元,面粉的保管與其費用為平均每天3元,購買面粉每次支付運費900元。
(1) 求該廠多少購買一次面粉才能使平均每天支付的總費用最小;
(2) 若提供面粉的公司規定,當一次購買面粉不少210噸時其價格可享受九折惠(即原價的90%)。問該廠是否考慮利用此優惠條件,請說明理由。
解(1)設該廠應隔x天購買一次面粉,其購買量為6x噸,則面粉的保管與其它費用
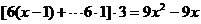 ,平均每天支出的費用為
,平均每天支出的費用為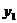 ,則
,則


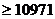

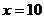
即每隔10天購買一次才能使平均每天支付的總費用最小。
(2)若廠家利用此優惠條件,則至少35天購買一次面粉,設該廠利用此優惠條件,每隔x天(x ) 購買一次面粉,平均每天支出的費用為
) 購買一次面粉,平均每天支出的費用為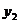 。
。

利用單調性可證
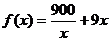 在
在 上遞增。
上遞增。
 時
時 取得最小值,即
取得最小值,即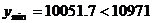 ,
,
 該廠應接受此優惠條件。
該廠應接受此優惠條件。
29. 某人拋擲一枚硬幣,出現正反的概率都是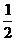 ,構造數列
,構造數列 ,使得
,使得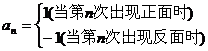 ,記
,記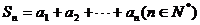 。
。
(1)
求 的概率;
的概率;
(2)
若前兩次均出現正面,求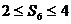 的概率。
的概率。
解:(1) ,需4次中有3次正面1次反面,設其概率為
,需4次中有3次正面1次反面,設其概率為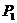
則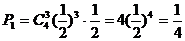
(2)6次中前兩次均出現正面,要使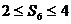 ,則后4次中有2次正面、2次反面或3次正面、1次反面。設其概率為
,則后4次中有2次正面、2次反面或3次正面、1次反面。設其概率為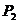 。
。
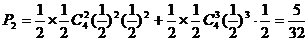
28.已知
且 (1)求
(1)求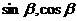 ; (2)求
; (2)求
解:(1)由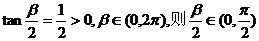



(2)由
則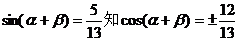
由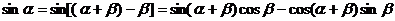
在 時,
時,
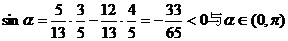 矛盾,故舍去.
矛盾,故舍去.
在 可取. 因此
可取. 因此
27. 若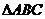 中,a,b,c分別是
中,a,b,c分別是 的對邊,且
的對邊,且 ,
,
(1)
求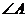 ;
;
(2)
若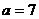 ,
,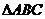 的面積為
的面積為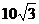 ,求b+c的值。
,求b+c的值。
解:(1)由 得:
得: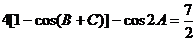 ,
,
可得: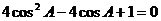 ,
, ,
,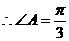 。
。
(2)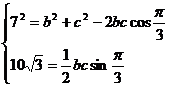
 ,
,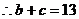 。
。
26. 如下圖,它滿足:
如下圖,它滿足:
(1) 第n行首尾兩數均為n ;
(2)表中的遞推關系類似楊輝三角.
則第n行(n≥2)第2個數是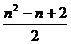 。
。
25.有一組數據: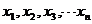
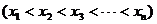 的算術平均值為10,若去掉其中最大的一個,余下數據的算術平均值為9;若去掉其中最小的一個,余下數據的算術平均值為11,第一個數
的算術平均值為10,若去掉其中最大的一個,余下數據的算術平均值為9;若去掉其中最小的一個,余下數據的算術平均值為11,第一個數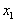 關于
關于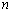 的表達式是
的表達式是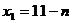 ,第
,第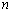 個數
個數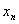 關于
關于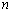 的表達式是
的表達式是 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com