日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

4.設A(x₁,x₂)、B(x₂,y₂)，則S_⊿AOB＝；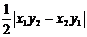

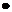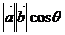3.設a=(x₁,y₁),b=(x₂,y₂),則ab==x₁x₂+y₁y₂;其幾何意義是a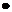b等于a的長度與b在a的方向上的投影的乘積；

2.兩個向量垂直的充要條件, 設a=(x₁,y₁),b=(x₂,y₂), (1)向量式：a⊥b(b≠0)a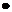b=0; (2)坐標式：a⊥bx₁x₂+y₁y₂=0;

1.兩個向量平行的充要條件,設a=(x₁,y₁),b=(x₂,y₂),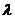為實數。(1)向量式：a∥b(b≠0)a=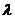b;(2)坐標式：a∥b(b≠0)x₁y₂－x₂y₁=0;

6.(1)正弦平方差公式：sin²A－sin²B=sin(A+B)sin(A－B);(2)三角形的內切圓半徑r=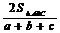；(3)三角形的外接圓直徑2R=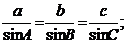

5.正(余)弦型函數的對稱軸為過最高點或最低點且垂直于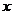軸的直線，對稱中心為圖象與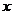軸的交點；正(余)切型函數的對稱中心是圖象和漸近線分別與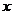軸的交點，但沒有對稱軸。

4.熟知正弦、余弦、正切的和、差、倍公式，正余弦定理，處理三角形內的三角函數問題勿忘三內角和等于180⁰，一般用正余弦定理實施邊角互化；

3.記住同角三角函數的基本關系，熟練掌握三角函數的定義、圖像、性質；

2.對于誘導公式，可用“奇變偶不變，符號看象限”概括；

1.三角函數符號規律記憶口訣：一全正，二正弦，三是切，四余弦；