
23.(2009重慶卷理)已知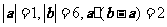 ,則向量
,則向量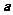 與向量
與向量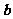 的夾角是( )
的夾角是( )
A.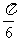 B.
B.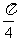 C.
C.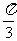 D.
D.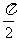


[答案]C
[解析]因為由條件得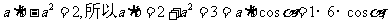
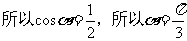
22.(2009福建卷文)設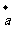 ,
,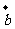 ,
,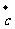 為同一平面內具有相同起點的任意三個非零向量,且滿足
為同一平面內具有相同起點的任意三個非零向量,且滿足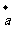 與
與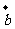 不共線,
不共線,
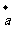
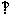
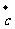 ∣
∣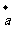 ∣=∣
∣=∣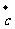 ∣,則∣
∣,則∣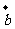 •
•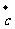 ∣的值一定等于
∣的值一定等于 

A.以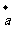 ,
,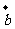 為鄰邊的平行四邊形的面積
B. 以
為鄰邊的平行四邊形的面積
B. 以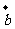 ,
,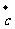 為兩邊的三角形面積
為兩邊的三角形面積
C.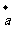 ,
,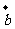 為兩邊的三角形面積
D. 以
為兩邊的三角形面積
D. 以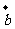 ,
,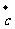 為鄰邊的平行四邊形的面積
為鄰邊的平行四邊形的面積
解析 假設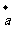 與
與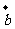 的夾角為
的夾角為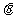 ,∣
,∣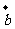 •
•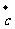 ∣=︱
∣=︱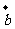 ︱·︱
︱·︱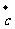 ︱·∣cos<
︱·∣cos<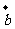 ,
,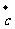 >∣=︱
>∣=︱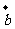 ︱·︱
︱·︱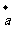 ︱•∣cos(90
︱•∣cos(90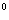

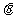 )∣=︱
)∣=︱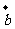 ︱·︱
︱·︱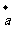 ︱•sin
︱•sin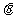 ,即為以
,即為以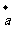 ,
,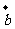 為鄰邊的平行四邊形的面積,故選A。
為鄰邊的平行四邊形的面積,故選A。
21.(2009湖南卷理)對于非0向時a,b,“a//b”的正確是 (A)
A.充分不必要條件 B. 必要不充分條件
C.充分必要條件 D. 既不充分也不必要條件
[答案]:A
[解析]由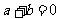 ,可得
,可得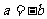 ,即得
,即得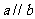 ,但
,但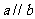 ,不一定有
,不一定有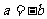 ,所以“
,所以“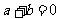 ”是“
”是“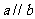 的充分不必要條件。
的充分不必要條件。
20.(2009寧夏海南卷文)已知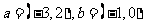 ,向量
,向量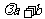 與
與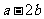 垂直,則實數
垂直,則實數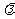 的值為
的值為
(A)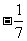 (B)
(B)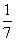 (C)
(C)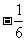 (D)
(D)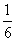
[答案]A
[解析]向量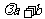 =(-3
=(-3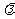 -1,2
-1,2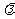 ),
),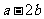 =(-1,2),因為兩個向量垂直,故有(-3
=(-1,2),因為兩個向量垂直,故有(-3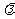 -1,2
-1,2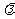 )×(-1,2)=0,即3
)×(-1,2)=0,即3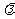 +1+4
+1+4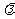 =0,解得:
=0,解得: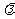 =
= ,故選.A。
,故選.A。
19.(2009陜西卷文)在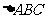 中,M是BC的中點,AM=1,點P在AM上且滿足
中,M是BC的中點,AM=1,點P在AM上且滿足 學
學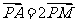 ,則科網
,則科網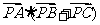 等于
等于
(A)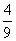 (B)
(B)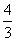 (C)
(C)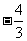 (D)
(D) 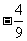

答案:A.
解析:由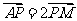 知,
知,
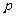 為
為 的重心,根據向量的加法,
的重心,根據向量的加法, 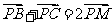 則
則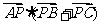 =
=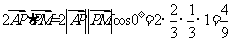
故選A
18.(2009全國卷Ⅰ文)設非零向量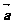 、
、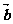 、
、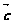 滿足
滿足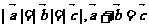 ,則
,則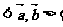
(A)150°B)120° (C)60° (D)30°
[解析]本小題考查向量的幾何運算、考查數形結合的思想,基礎題。
解:由向量加法的平行四邊形法則,知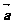 、
、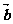 可構成菱形的兩條相鄰邊,且
可構成菱形的兩條相鄰邊,且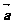 、
、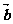 為起點處的對角線長等于菱形的邊長,故選擇B。
為起點處的對角線長等于菱形的邊長,故選擇B。
17.(2009遼寧卷文)平面向量a與b的夾角為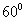 ,a=(2,0), | b |=1,則 | a+2b |=
,a=(2,0), | b |=1,則 | a+2b |=
(A)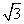 (B)2
(B)2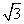 (C)4 (D)12
(C)4 (D)12
[解析]由已知|a|=2,|a+2b|2=a2+4a·b+4b2=4+4×2×1×cos60°+4=12
∴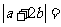
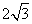
[答案]B
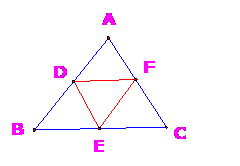
16.(2009湖南卷文)如圖1, D,E,F分別是 ABC的邊AB,BC,CA的中點,則[
A ]
ABC的邊AB,BC,CA的中點,則[
A ]
 A.
A.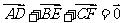
B.
C.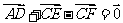
D.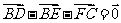
圖1
解: 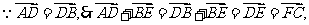 得
得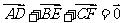 ,故選A.
,故選A.
或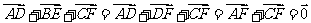 .
.
15.(2009湖北卷文)若向量a=(1,1),b=(-1,1),c=(4,2),則c=
A.3a+b B. 3a-b C.-a+3b D. a+3b
[答案]B
[解析]由計算可得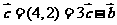 故選B
故選B
14.(2009寧夏海南卷理)已知O,N,P在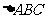 所在平面內,且
所在平面內,且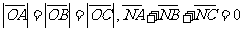 ,且
,且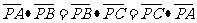 ,則點O,N,P依次是
,則點O,N,P依次是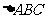 的
的
(A)重心 外心 垂心 (B)重心 外心 內心
(C)外心 重心 垂心 (D)外心 重心 內心
(注:三角形的三條高線交于一點,此點為三角型的垂心)
解析:
 ;
;

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com