
18.(本題滿分13分)
根據氣象預報,某地區近期有小洪水的概率為0.25,有大洪水的概率為0.01.該地區某工地上有一臺大型設備,遇到大洪水時要損失60000元,遇到小洪水時要損失10000元.為保護設備,有以下3種方案:
方案1:運走設備,搬運費為3800元.
方案2:建保護墻,建設費為2000元.但圍墻只能防小洪水.
方案3:不采取措施,希望不發生洪水.
試比較哪一種方案好?
17.(本題滿分13分)
袋中有20個大小相同的球,其中記上0號的有10個,記上 號的有
號的有 個(
個(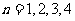 ).現從袋中任意取一球,
).現從袋中任意取一球,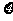 表示所取球的標號.
表示所取球的標號.
(1)求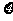 的分布列、期望和方差;
的分布列、期望和方差;
(2)若 ,
,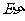 =1,
=1, =11,試求
=11,試求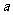 、
、 的值.
的值.
16.(本題滿分13分)
 已知
已知 是
是
 內任意一點,連結
內任意一點,連結 ,
,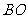 ,
,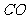 并延長交對邊于
并延長交對邊于 ,
, ,
,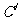 ,則
,則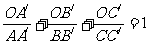 . 這是平面幾何中的一個命題,其證明方法常采用“面積法”:
. 這是平面幾何中的一個命題,其證明方法常采用“面積法”: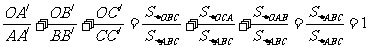 .運用類比猜想,對于空間四面體存在什么類似的命題?并用“體積法”證明.
.運用類比猜想,對于空間四面體存在什么類似的命題?并用“體積法”證明.
15.(本題滿分13分)
一臺機器使用的時間較長,但還可以使用,它按不同的轉速生產出來的某機械零件有一些會有缺點,每小時生產有缺點零件的多少,隨機器的運轉的速度而變化,下表為抽樣試驗的結果:
|
轉速x(轉/秒) |
16 |
14 |
12 |
8 |
|
每小時生產有缺點的零件數y(件) |
11 |
9 |
8 |
5 |
(1)利用散點圖或相關系數r的大小判斷變量y對x是否線性相關?為什么?
(2)如果y對x有線性相關關系,求回歸直線方程;
(3)若實際生產中,允許每小時的產品中有缺點的零件最多為10個,那么機器的運轉速度應控制在什么范圍內?(最后結果精確到0.001.參考數據: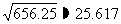 ,
,
 ,
, ,
, =291).
=291).
14.從以下三個小題中選做一題(請回答且只能回答其中一個,回答兩個或兩個以上的,按得分最低的記分).
(1)(不等式選講選做題)已知 ,若關于
,若關于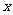 的方程
的方程 有實根,則
有實根,則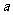 的取值范圍是 .
的取值范圍是 .
(2)(坐標系與參數方程選做題)已知曲線 、
、 的極坐標方程分別為
的極坐標方程分別為 ,
,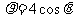
 ,則曲線
,則曲線 、
、 交點的極坐標為 .
交點的極坐標為 .
(3)(幾何證明選講選做題)已知PA是圓O的切線,切點為A,PA=2.AC是圓O的直徑,PC與圓O交于點B,PB=1,則圓O的半徑R= .
13.若函數f(x)=x3-3a2x+1的圖象與直線y=3只有一個公共點,則實數a的取值范圍為__________.
12.從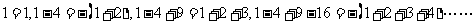 概括出第
概括出第 個式子為___________.
個式子為___________.
11. 某地奧運火炬接力傳遞路線共分6段,傳遞活動分別由6名火炬手完成.如果第一棒火炬手只能從甲、乙、丙三人中產生,最后一棒火炬手只能從甲、乙兩人中產生,則不同的傳遞方案共有_________種.(用數字作答).
10.設 ,則
,則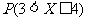 = .
= .
9. 已知復數 是純虛數,則實數
是純虛數,則實數 = .
= .
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com