
題目列表(包括答案和解析)
(08年潮州市二模理)(14分)已知函數![]() 的導數
的導數![]() 滿足
滿足![]() ,常數
,常數![]() 為方程
為方程![]() 的實數根.
的實數根.
⑴ 若函數![]() 的定義域為I,對任意
的定義域為I,對任意![]() ,存在
,存在![]() ,使等式
,使等式![]() =
=![]() 成立,
成立,
求證:方程![]() 不存在異于
不存在異于![]() 的實數根;
的實數根;
⑵ 求證:當![]() 時,總有
時,總有![]() 成立;
成立;
⑶ 對任意![]() ,若滿足
,若滿足![]() ,求證
,求證![]() .
.
22已知函數![]() ,若方程
,若方程![]() 有且只有兩個相異根0和2,且
有且只有兩個相異根0和2,且![]()
(1)求函數![]() 的解析式。
的解析式。
(2)已知各項不為1的數列{an}滿足![]() ,求數列通項an。
,求數列通項an。
(3)如果數列{bn}滿足![]() ,求證:當
,求證:當![]() 時,恒有
時,恒有![]() 成立。
成立。
(本小題滿分12分)
對于函數f(x),若存在x0∈R,使f(x0)=x0成立,則稱x0為f(x)的不動點。如果函數 有且只有兩個不動點0,2,且
有且只有兩個不動點0,2,且
(1)求函數f(x)的解析式;
(2)已知各項不為零的數列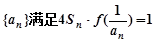 (
( 為
為 數列前n項和),求數列通項
數列前n項和),求數列通項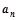 ;
;
(3)如果數列 滿足
滿足 ,求證:當
,求證:當 時,恒有
時,恒有 成立.
成立.
已知函數![]() 的導函數
的導函數![]() 滿足
滿足![]() 常數
常數![]() 為方程
為方程![]()
的實數根
(1)若函數![]() 的定義域為I,對任意
的定義域為I,對任意![]() 存在
存在![]() 使等式
使等式![]() 成立。 求證:方程
成立。 求證:方程![]() 不存在異于
不存在異于![]() 的實數根。
的實數根。
(2)求證:當![]() 時,總有
時,總有![]() 成立。
成立。
(本小題滿分14分)已知定義在 上的函數
上的函數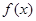 ,滿足條件:①
,滿足條件:① ,②對非零實數
,②對非零實數 ,都有
,都有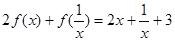 .
.
(1)求函數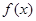 的解析式;
的解析式;
(2)設函數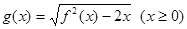 ,直線
,直線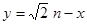 分別與函數
分別與函數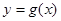 ,
,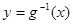 交于
交于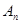 、
、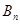 兩點,(其中
兩點,(其中 );設
);設 ,
,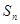 為數列
為數列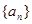 的前
的前 項和,求證:當
項和,求證:當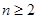 時,
時,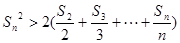 .
.
一.選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
B
A
C
D
D
D
A
B
A
A
二.填空題
13.4; 14.  ; 15.15; 16.
; 15.15; 16. ,
, 可以填寫任一實數.
可以填寫任一實數.
三.解答題
17. (Ⅰ)列表:


2
6
10
14

0





1
3
1

1
描點作圖,得圖象如下.
 6分
6分
(Ⅱ)

所以,當 ,即
,即 時,函數
時,函數 取得最小值
取得最小值 . 12分
. 12分
18.由圖可知,參加活動1次、2次和3次的學生人數分別為5、25和20.
(I)該班學生參加活動的人均次數為 =
= . 6分
. 6分
(II)從該班中任選兩名學生,他們參加活動次數恰好相等的概率為 .
12分
.
12分
19.(Ⅰ)∵AD=2AB=2,E是AD的中點,
∴△BAE,△CDDE是等腰直角三角形,
易知,∠BEC=90°,即BE⊥EC
又∵平面D′EC⊥平面BEC,面D′EC∩面BEC=EC,
∴BE⊥面D′EC,又CD′ 面D′EC,∴BE⊥CD′.
6分
面D′EC,∴BE⊥CD′.
6分
(Ⅱ)法一:設M是線段EC的中點,過M作MF⊥BC
垂足為F,連接D′M,D′F,則D′M⊥EC
∵平面D′EC⊥平面BEC,
 ∴D′M⊥平面EBC,
∴D′M⊥平面EBC,
∴MF是D′F在平面BEC上的射影,
由三垂線定理得:D′F⊥BC
∴∠D′FM是二面D′―BC―E的平面角.
在Rt△D′MF中,
∴ ,
,
即二面角D′―BC―E的正切值為 .
12分
.
12分
法二:如圖,以EB,EC為x軸,y軸,過E垂直于平面BEC的射線為z軸,建立空間直角坐標系,
則
設平面BEC的法向量為 ;平面D′BC的法向量為
;平面D′BC的法向量為


由
取
∴

∴二面角D′―BC―E的正切值為 .
12分
.
12分
20.(I) ,
,

(II) 由(I)知
由(I)知


21(Ⅰ)設橢圓C的方程為 ,則由題意知b = 1.
,則由題意知b = 1.

∴橢圓C的方程為
 …………………………………………………6分
…………………………………………………6分
(Ⅱ)易知直線 的斜率為
的斜率為 ,從而直線
,從而直線 的斜率為1.設直線的方程為
的斜率為1.設直線的方程為 ,代如橢圓的方程,并整理可得
,代如橢圓的方程,并整理可得 .設
.設 ,則
,則 ,
, .于是
.于是


解之得 或
或 .
.
當 時,點
時,點 即為直線
即為直線 與橢圓的交點,不合題意.當
與橢圓的交點,不合題意.當 時,經檢驗知
時,經檢驗知 和橢圓相交,符合題意.
和橢圓相交,符合題意.
所以,當且僅當直線 的方程為
的方程為 時, 點
時, 點 是
是 的垂心. 12分
的垂心. 12分
22.(Ⅰ)對一切 有
有

于是, 

 (
( ) 5分
) 5分
(Ⅱ)由 及
及
兩式相減,得: 


∴ . 10分
. 10分
(Ⅲ) 由于 ,
,
所以, 14分
14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com