
題目列表(包括答案和解析)
| 5π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
 -2x)是偶函數;
-2x)是偶函數; )的表達式可以改寫成f(x)=4cos(2x-
)的表達式可以改寫成f(x)=4cos(2x- )
) .
.關于函數![]() ,有下列命題:
,有下列命題:
① 其最小正周期為![]() ;② 其圖像由
;② 其圖像由![]() 個單位而得到;
個單位而得到;
③ 其表達式寫成![]() ④ 在
④ 在![]() 為單調遞增函數.則其中真命題為 .
為單調遞增函數.則其中真命題為 .
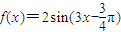 ,有下列命題:
,有下列命題: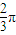 ;
; 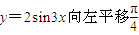 個單位而得到;
個單位而得到;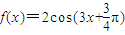 ;
;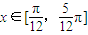 為單調遞增函數;
為單調遞增函數;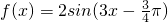 ,有下列命題:
,有下列命題: ;
; 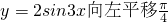 個單位而得到;
個單位而得到;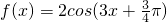 ;
;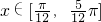 為單調遞增函數;
為單調遞增函數;一、選擇題(60分)
BCCA BDAB BAAA
二、填空題(16分)
13、
14、0
15、1
16、
三、解答題(74分)
17、解(1) ,
,
∴遞增區間為 ----------------------6分
----------------------6分
(2)
而 ,
,
故 --------------- 12分
--------------- 12分
18、解:(1)3個旅游團選擇3條不同線路的概率為:P1= …………3分
…………3分
(2)恰有兩條線路沒有被選擇的概率為:P2= ……6分
……6分
(3)設選擇甲線路旅游團數為ξ,則ξ=0,1,2,3
P(ξ=0)= P(ξ=1)=
P(ξ=1)=
P(ξ=2)=  P(ξ=3)=
P(ξ=3)= 
ξ
0
1
2
3




∴ξ的分布列為:
∴期望Eξ=0× +1×
+1× +2×
+2× +3×
+3× =
= ………………12分
………………12分
19、
|