圖②
方法二:如圖②,延長BC、AE相交于點P
∵在□ABCD中,AD∥BC
∴∠DAP=∠APB
…………………………1分
∵AE平分∠DAB
∴∠DAP=∠PAB
…………………………2分
∴∠APB=∠PAB
∴AB=BP
………………………3分
∵BF平分∠ABP
∴:AP⊥BF
即AE⊥BF.
………………………4分
(2)方法一:線段DF與CE是相等關系,即DF=CE ………………5分
∵在□ABCD中,CD∥AB
∴∠DEA=∠EAB
又∵AE平分∠DAB
∴∠DAE=∠EAB
∴∠DEA=∠DAE
∴DE=AD ………………………6分
同理可得,CF=BC ………………………7分
又∵在□ABCD中,AD=BC
∴DE=CF
∴DE-EF=CF-EF
即DF=CE.
………………………8分
方法二:如右圖,延長BC、AE設交于點P,延長AD、BF相交于點O …5分
.files/image767.gif) ∵在□ABCD中,AD∥BC
∵在□ABCD中,AD∥BC
∴∠DAP=∠APB
∵AE平分∠DAB
∴∠DAP=∠PAB
∴∠APB=∠PAB
∴BP=AB
同理可得,AO=AB
∴AO=BP ………………………6分
∵在□ABCD中,AD=BC
∴OD=PC
又∵在□ABCD中,DC∥AB
∴△ODF∽△OAB,△PCE∽△PBA ………………………7分
∴.files/image769.gif) =
=.files/image771.gif) ,
,.files/image773.gif) =
=.files/image775.gif)
∴DF=CE.
………………………8分
6. (1)(2)略 (3)設BC=x,則DC=x ,BD=.files/image777.gif) ,CF=(
,CF=(.files/image171.gif) -1)x
-1)x
GD2=GE?GB=4-2.files/image171.gif) DC2+CF2=(2GD)2 即 x2+(
DC2+CF2=(2GD)2 即 x2+(.files/image171.gif) -1)2x2=4(4-2
-1)2x2=4(4-2.files/image171.gif) )
)
(4-2.files/image171.gif) )x2=4(4-2
)x2=4(4-2.files/image171.gif) ) x2=4 正方形ABCD的面積是4個平方單位
) x2=4 正方形ABCD的面積是4個平方單位
7.(本小題滿分5分)
.files/image780.gif) 證明:∵ AB∥CD
證明:∵ AB∥CD
∴ .files/image782.gif) …………1分
…………1分
.files/image780.gif) ∵
∵ .files/image784.gif)
∴ △ABO≌△CDO
…………3分
∴ .files/image786.gif) …………4分
…………4分
∴ 四邊形ABCD是平行四邊形 …………5分
.files/image788.jpg)
.files/image790.jpg)
.files/image792.jpg)
.files/image794.jpg)
11.證明:(1)①在.files/image044.gif) 和
和.files/image797.gif) 中,
中,
.files/image189.gif) ,
,.files/image191.gif) ,
,.files/image801.gif) ,????????????????????????????????????????????????????????????????????????? 2分
,????????????????????????????????????????????????????????????????????????? 2分
.files/image803.gif) .????????????????????????????????????????????????????????????????????????????????????????????????? 3分
.????????????????????????????????????????????????????????????????????????????????????????????????? 3分
②.files/image805.gif) ,
,
.files/image807.gif) .?????????????????????????????????????????????????????????????????????????????????????????????????? 4分
.?????????????????????????????????????????????????????????????????????????????????????????????????? 4分
.files/image809.gif) ,
,
12.(本題7分)
解:(1)在梯形.files/image125.gif) 中,
中,.files/image217.gif) ,
,
.files/image219.gif) ,
,.files/image814.gif) ,
,
.files/image816.gif) ,
,
.files/image818.gif) .
.
.files/image820.gif) ,
,
.files/image822.gif) ,
,
.files/image824.gif) .
.
.files/image826.gif) .?????????????????????????????????????????????????????????????????????????????????????????????????? 2分
.?????????????????????????????????????????????????????????????????????????????????????????????????? 2分
.files/image828.gif) .???????????????????????????????????????????????????????????????????????????????????????????????????????????? 3分
.???????????????????????????????????????????????????????????????????????????????????????????????????????????? 3分
.files/image830.gif) ,
,.files/image235.gif) ,
,
.files/image833.gif) .?????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
.?????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
.files/image835.gif)
.files/image237.gif) 與
與.files/image179.gif) 的函數表達式是
的函數表達式是
.files/image839.gif) ;??????????????????????????????????????????????????????????????????????????????????????? 5分
;??????????????????????????????????????????????????????????????????????????????????????? 5分
(2).files/image841.gif)
.files/image843.gif) .?????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
.?????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
.files/image835.gif) 當
當.files/image846.gif) 時,
時,.files/image237.gif) 有最大值,最大值為
有最大值,最大值為.files/image849.gif) .??????????????????????????????????????????????????????????????????? 7分
.??????????????????????????????????????????????????????????????????? 7分
13.證明:菱形.files/image125.gif) 中,
中,.files/image852.gif) .???????????????????? 1分
.???????????????????? 1分
.files/image854.gif) 分別是
分別是.files/image856.gif) 的中點,
的中點,
.files/image858.gif) .?????????????????? 3分
.?????????????????? 3分
又.files/image860.gif) ,
,.files/image862.gif) .????????????????? 5分
.????????????????? 5分
.files/image864.gif) .??????????????????????????????? 7分
.??????????????????????????????? 7分
14.
.files/image866.jpg)
15.證明:.files/image868.gif) 四邊形
四邊形.files/image125.gif) 是平行四邊形,
是平行四邊形,.files/image871.gif) ,
,.files/image873.gif) .
.
.files/image875.gif) .??????????????????????????????????????????????????????????????????????????????????????????????????? 1分
.??????????????????????????????????????????????????????????????????????????????????????????????????? 1分
.files/image877.gif) 平分
平分.files/image254.gif) ,
,.files/image880.gif) .????????????????????????????????????????????????????????????????? 2分
.????????????????????????????????????????????????????????????????? 2分
.files/image882.gif) .??????????????????????????????????????????????????????????????????????????????????????????????????? 3分
.??????????????????????????????????????????????????????????????????????????????????????????????????? 3分
.files/image884.gif) .??????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
.??????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
又.files/image886.gif) ,
,.files/image888.gif) .???????????????????????????????????????????????????????????????????????????????????? 5分
.???????????????????????????????????????????????????????????????????????????????????? 5分
16.解:(1)①40.?????????????????????????????????????????????????????????????????????????????????????????????????????? 2分
②0. ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
(2)不合理.例如,對兩個相似而不全等的矩形來說,它們接近正方形的程度是相同的,但.files/image284.gif) 卻不相等.合理定義方法不唯一,如定義為
卻不相等.合理定義方法不唯一,如定義為.files/image891.gif) .
..files/image891.gif) 越小,矩形越接近于正方形;
越小,矩形越接近于正方形;.files/image891.gif) 越大,矩形與正方形的形狀差異越大;當
越大,矩形與正方形的形狀差異越大;當.files/image895.gif) 時,矩形就變成了正方形.???????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
時,矩形就變成了正方形.???????????????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
17.解:(1).files/image868.gif) 正方形
正方形.files/image125.gif) 中,
中,.files/image304.gif) ,
,.files/image900.gif) .
.
.files/image901.gif) 又
又.files/image308.gif) ,因此
,因此.files/image904.gif) ,即菱形
,即菱形.files/image297.gif) 的邊長為
的邊長為.files/image907.gif) .
.
在.files/image909.gif) 和
和.files/image911.gif) 中,
中,.files/image913.gif) ,
,
.files/image915.gif) ,
,.files/image917.gif) ,
,
.files/image919.gif) .
..files/image921.gif) .
.
.files/image923.gif) ,
,.files/image925.gif) ,
,
.files/image927.gif) ,即菱形
,即菱形.files/image297.gif) 是正方形.
是正方形.
同理可以證明.files/image930.gif) .
.
因此.files/image932.gif) ,即點
,即點.files/image471.gif) 在
在.files/image084.gif) 邊上,同時可得
邊上,同時可得.files/image936.gif) ,
,
從而.files/image938.gif) .????????????????????????????????????????????????????????????????????????????????????????? 2分
.????????????????????????????????????????????????????????????????????????????????????????? 2分
.files/image940.gif) (2)作
(2)作.files/image942.gif) ,
,.files/image431.gif) 為垂足,連結
為垂足,連結.files/image945.gif) ,
,
.files/image947.gif) ,
,.files/image949.gif) ,
,
.files/image951.gif) ,
,.files/image953.gif) .
.
.files/image955.gif) .
.
在.files/image909.gif) 和
和.files/image958.gif) 中,
中,.files/image960.gif) ,
,.files/image962.gif) ,
,
.files/image964.gif) .
.
.files/image966.gif) ,即無論菱形
,即無論菱形.files/image297.gif) 如何變化,點
如何變化,點.files/image471.gif) 到直線
到直線.files/image244.gif) 的距離始終為定值2.
的距離始終為定值2.
因此.files/image971.gif) .??????????????????????????????????????????????????????????????????????????? 6分
.??????????????????????????????????????????????????????????????????????????? 6分
(3)若.files/image973.gif) ,由
,由.files/image975.gif) ,得
,得.files/image977.gif) ,此時,在
,此時,在.files/image911.gif) 中,
中,.files/image980.gif) .
.
相應地,在.files/image909.gif) 中,
中,.files/image983.gif) ,即點
,即點.files/image227.gif) 已經不在邊
已經不在邊.files/image082.gif) 上.
上.
故不可能有.files/image973.gif) .???????????????????????????????????????????????????????????????????????????????????????????????? 9分
.???????????????????????????????????????????????????????????????????????????????????????????????? 9分
另法:由于點.files/image577.gif) 在邊
在邊.files/image734.gif) 上,因此菱形的邊長至少為
上,因此菱形的邊長至少為.files/image990.gif) ,
,
當菱形的邊長為4時,點.files/image227.gif) 在
在.files/image082.gif) 邊上且滿足
邊上且滿足.files/image994.gif) ,此時,當點
,此時,當點.files/image227.gif) 逐漸向右運動至點
逐漸向右運動至點.files/image424.gif) 時,
時,.files/image998.gif) 的長(即菱形的邊長)將逐漸變大,最大值為
的長(即菱形的邊長)將逐漸變大,最大值為.files/image1000.gif) .
.
此時,.files/image1002.gif) ,故
,故.files/image1004.gif) .
.
而函數.files/image975.gif) 的值隨著
的值隨著.files/image179.gif) 的增大而減小,
的增大而減小,
因此,當.files/image1008.gif) 時,
時,.files/image1010.gif) 取得最小值為
取得最小值為.files/image1012.gif) .
.
又因為.files/image1014.gif) ,所以,
,所以,.files/image310.gif) 的面積不可能等于1.????????????????????? 9分
的面積不可能等于1.????????????????????? 9分
18.
.files/image1017.jpg)
.files/image1019.jpg)
19.證明:在等腰.files/image044.gif) 中,
中,.files/image104.gif) ,
,.files/image1023.gif) .
.
.files/image1025.gif) ,
,.files/image325.gif) ,
,.files/image1028.gif) .又
.又.files/image1030.gif) ,
,
.files/image1032.gif) .????????????????????????????????????????????????????????????????????????? 3分
.????????????????????????????????????????????????????????????????????????? 3分
.files/image888.gif) .
..files/image1035.gif) .
.
.files/image1037.gif) .
..files/image1039.gif) .
..files/image1041.gif) .?????????????????? 5分
.?????????????????? 5分
又.files/image1043.gif) 不平行,
不平行,.files/image835.gif) 四邊形
四邊形.files/image333.gif) 是梯形.??????????????????????????????????? 7分
是梯形.??????????????????????????????????? 7分
.files/image835.gif) 四邊形
四邊形.files/image333.gif) 是等腰梯形.(理由:同一底上的兩底角相等的梯形是等腰梯形,或兩腰相等的梯形是等腰梯形)?????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
是等腰梯形.(理由:同一底上的兩底角相等的梯形是等腰梯形,或兩腰相等的梯形是等腰梯形)?????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
20.解:(1)在矩形.files/image337.gif) 中,
中,.files/image868.gif)
.files/image1051.gif) ,
,.files/image1053.gif) ,
,
.files/image1055.gif) .……………………1分
.……………………1分
.files/image1057.gif) ,
,.files/image1059.gif) .
.
.files/image1061.gif) ,即
,即.files/image1063.gif) ,
,


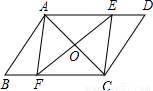
 24、如圖,平行四邊形ABCD中,點E、F分別在BC,AD上,且AE∥CF.求證:∠AFC=∠AEC.
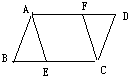
24、如圖,平行四邊形ABCD中,點E、F分別在BC,AD上,且AE∥CF.求證:∠AFC=∠AEC.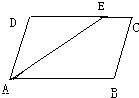 8、如圖,平行四邊形ABCD中,AD=6cm,AB=9cm,AE平分∠DAB,則CE=
8、如圖,平行四邊形ABCD中,AD=6cm,AB=9cm,AE平分∠DAB,則CE=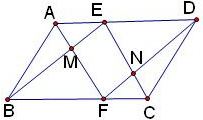 22、如圖,平行四邊形ABCD中,E、F為邊AD、BC上的點,且AE=CF,連接AF、EC、BE、DF交于M、N,試說明:MFNE是平行四邊形.
22、如圖,平行四邊形ABCD中,E、F為邊AD、BC上的點,且AE=CF,連接AF、EC、BE、DF交于M、N,試說明:MFNE是平行四邊形..files/image745.jpg)
.files/image747.gif) -2
-2 .files/image749.jpg)
.files/image751.gif)
.files/image754.gif)
.files/image756.gif) ,
,.files/image758.gif) .所以周長最大值為17.-------------------------------------------9分
.所以周長最大值為17.-------------------------------------------9分.files/image760.jpg)
.files/image762.jpg)
.files/image764.gif) ∴AE⊥BF.
…………………………4分
∴AE⊥BF.
…………………………4分.files/image765.gif)