
題目列表(包括答案和解析)
 (a>0,b>0)的離心率為
(a>0,b>0)的離心率為 ,且過點(4,3).
,且過點(4,3). (a>0,b>0)的右準線與一條漸近線交于點M,F是右焦點,若|MF|=1,且雙曲線C的離心率
(a>0,b>0)的右準線與一條漸近線交于點M,F是右焦點,若|MF|=1,且雙曲線C的離心率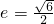 .
.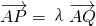 且
且 ,求直線l斜率k的取值范圍.
,求直線l斜率k的取值范圍. (a>0,b>0)
(a>0,b>0)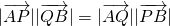 ,求證點Q總在某定直線上.
,求證點Q總在某定直線上. (a>0,b>0),過雙曲線外一點P(m,n)的動直線l與雙曲線C相交與不同兩點A,B時,在線段AB上取點Q,滿足
(a>0,b>0),過雙曲線外一點P(m,n)的動直線l與雙曲線C相交與不同兩點A,B時,在線段AB上取點Q,滿足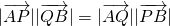 ,則點Q在哪條定直線上?
,則點Q在哪條定直線上? (a>0,b>0)的離心率為
(a>0,b>0)的離心率為 ,右準線方程為
,右準線方程為 。
。 (a>0,b>0),F1、F2分別為C 的左、右焦點。P為C右支上一點,且使∠F1PF2=
(a>0,b>0),F1、F2分別為C 的左、右焦點。P為C右支上一點,且使∠F1PF2= ,又 △F1PF2的面積為
,又 △F1PF2的面積為 。
。1.(文)A(理)C 2.(文)A(理)B 3.C 4.(文)D(理)B
5.(文)D (理)C 6.A 7.C 8.B 9.A 10.D 11.A 12.C
13.33 14.7 15.18
16.只要寫出
17.解析:



 .
.
18.解析:(1)由 ,
, ,
, 成等差數列,得
成等差數列,得 ,
,
若q=1,則 ,
, ,
,
由 ≠0 得
≠0 得  ,與題意不符,所以q≠1.
,與題意不符,所以q≠1.
由 ,得
,得 .
.
整理,得 ,由q≠0,1,得
,由q≠0,1,得 .
.
(2)由(1)知: ,
,
 ,所以
,所以 ,
, ,
, 成等差數列.
成等差數列.
19.解析:(1)記“摸出兩個球,兩球恰好顏色不同”為A,摸出兩個球共有方法 種,
種,
其中,兩球一白一黑有 種.
種.
∴  .
.
(2)法一:記摸出一球,放回后再摸出一個球“兩球恰好顏色不同”為B,摸出一球得白球的概率為 ,摸出一球得黑球的概率為
,摸出一球得黑球的概率為 ,
,
∴ P(B)=0.4×0.6+0.6+×0.4=0.48
法二:“有放回摸兩次,顏色不同”指“先白再黑”或“先黑再白”.
∴ 
∴ “有放回摸兩次,顏色不同”的概率為 .
.
20.解析:(甲)(1)∵ △ 為以點M為直角頂點的等腰直角三角形,∴
為以點M為直角頂點的等腰直角三角形,∴  且
且 .
.
∵ 正三棱柱 , ∴
, ∴  底面ABC.
底面ABC.
∴  在底面內的射影為CM,AM⊥CM.
在底面內的射影為CM,AM⊥CM.
∵ 底面ABC為邊長為a的正三角形, ∴ 點M為BC邊的中點.

(2)過點C作CH⊥ ,由(1)知AM⊥
,由(1)知AM⊥ 且AM⊥CM,
且AM⊥CM,
∴ AM⊥平面 ∵ CH在平面
∵ CH在平面 內, ∴ CH⊥AM,
內, ∴ CH⊥AM,
∴ CH⊥平面 ,由(1)知,
,由(1)知, ,
, 且
且 .
.
∴  . ∴
. ∴  .
.
∴ 點C到平面 的距離為底面邊長為
的距離為底面邊長為 .
.
(3)過點C作CI⊥ 于I,連HI, ∵ CH⊥平面
于I,連HI, ∵ CH⊥平面 ,
,
∴ HI為CI在平面 內的射影,
內的射影,
∴ HI⊥ ,∠CIH是二面角
,∠CIH是二面角 的平面角.
的平面角.
在直角三角形 中,
中, ,
,

 ,
,
∴ ∠CIH=45°, ∴ 二面角 的大小為45°
的大小為45°
(乙)解:(1)以B為原點,建立如圖所示的空間直角坐標系.

∵ AC=
∴  .
.
∴ B(0,0,0),C(0, ,0),A(
,0),A( ,0,0),
,0,0),
 (
( ,0,
,0, (0,
(0, ,
, (0,0,
(0,0,
∴  ,
, ,
, ,
, ,
, ,
, ,
,
∴  ,
, ,
, ,
,
 ,
, ,
, .
.
∴  ,
,
 , ∴
, ∴  ,
,

∴  . 故BE與
. 故BE與 所成的角為
所成的角為 .
.
(2)假設存在點F,要使CF⊥平面 ,只要
,只要 且
且 .
.
不妨設AF=b,則F( ,0,b),
,0,b), ,
, ,
, ,
, ,0,
,0, ,
,
 ,
, ,
, , ∵
, ∵  , ∴
, ∴  恒成立.
恒成立.
 或
或 ,
,
故當 或
或 平面
平面 .
.
21.解析:(1)法一:l: ,
,
解得 ,
, . ∵
. ∵  、
、 、
、 成等比數列,
成等比數列,
∴  ,
, ∴
∴  ,
,
 ,
, ,
, ,
, ,
,
∴  ,
, . ∴
. ∴ 
法二:同上得 ,
, .
.
∴ PA⊥x軸. . ∴
. ∴  .
.
(2) ∴
∴  .
.
即  , ∵
, ∵  ,
,
∴  ,即
,即  ,
, . ∴
. ∴  ,即
,即  .
.
22.解析:(1) . 又c<b<1,
. 又c<b<1,
故 方程f(x)+1=0有實根,
方程f(x)+1=0有實根,
即 有實根,故△=
有實根,故△=
即 或
或
又c<b<1,得-3<c≤-1,由 知
知 .
.
(2) ,
, .
.
∴ c<m<1 ∴  .
.
∴  . ∴
. ∴  的符號為正.
的符號為正.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com