
題目列表(包括答案和解析)
 是位于這個(gè)三角形數(shù)表中從上往下數(shù)第
是位于這個(gè)三角形數(shù)表中從上往下數(shù)第 行,從左向右數(shù)第
行,從左向右數(shù)第 個(gè)數(shù)。
個(gè)數(shù)。 
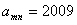 ,求m,n的值;
,求m,n的值; 的反函數(shù)為
的反函數(shù)為 ,若記三角形數(shù)表中從上往下數(shù)第n行各數(shù)的和為
,若記三角形數(shù)表中從上往下數(shù)第n行各數(shù)的和為 。
。  的前n項(xiàng)的和
的前n項(xiàng)的和 。
。 ,設(shè)
,設(shè) 的前n項(xiàng)之積為
的前n項(xiàng)之積為 ,求證:
,求證: 。
。 定義:若數(shù)列![]() 滿足
滿足![]() ,則稱(chēng)數(shù)列
,則稱(chēng)數(shù)列![]() 為“平方數(shù)列”。已知數(shù)列
為“平方數(shù)列”。已知數(shù)列![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 在函數(shù)
在函數(shù)![]() 的圖像上,其中
的圖像上,其中![]() 為正整數(shù)。
為正整數(shù)。
⑴證明:數(shù)列![]() 是“平方數(shù)列”,且
是“平方數(shù)列”,且![]() 數(shù)列
數(shù)列![]() 為等比數(shù)列。
為等比數(shù)列。
⑵設(shè)![]() ⑴中“平方數(shù)列”的前
⑴中“平方數(shù)列”的前![]() 項(xiàng)之積為
項(xiàng)之積為![]() ,即
,即![]() ,求數(shù)列
,求數(shù)列![]() 的通項(xiàng)及
的通項(xiàng)及![]() 關(guān)于
關(guān)于![]() 的表達(dá)式。
的表達(dá)式。
⑶記![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項(xiàng)之和
項(xiàng)之和![]() ,并求使
,并求使![]() 的
的![]() 的最小值。
的最小值。
由函數(shù)![]() 確定數(shù)列
確定數(shù)列![]() ,
,![]() ,函數(shù)
,函數(shù)![]() 的反函數(shù)
的反函數(shù)![]() 能確定數(shù)列
能確定數(shù)列![]() ,
,![]() ,若對(duì)于任意
,若對(duì)于任意![]() ,都有
,都有![]() ,則稱(chēng)數(shù)列
,則稱(chēng)數(shù)列![]() 是數(shù)列
是數(shù)列![]() 的“自反數(shù)列”。
的“自反數(shù)列”。
(1)若函數(shù)![]() 確定數(shù)列
確定數(shù)列![]() 的自反數(shù)列為
的自反數(shù)列為![]() ,求
,求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)在(1)條件下,記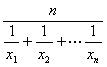 為正數(shù)數(shù)列
為正數(shù)數(shù)列![]() 的調(diào)和平均數(shù),若
的調(diào)和平均數(shù),若![]() ,
,
![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項(xiàng)和,
項(xiàng)和,![]() 為數(shù)列
為數(shù)列![]() 的調(diào)和平均數(shù),求
的調(diào)和平均數(shù),求![]() ;
;
(3)已知正數(shù)數(shù)列![]() 的前
的前![]() 項(xiàng)之和
項(xiàng)之和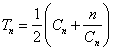 。求
。求![]() 的表達(dá)式。
的表達(dá)式。
已知公比為![]() 的無(wú)窮等比數(shù)列
的無(wú)窮等比數(shù)列![]() 各項(xiàng)的和為9,無(wú)窮等比數(shù)列
各項(xiàng)的和為9,無(wú)窮等比數(shù)列![]() 各項(xiàng)的和為
各項(xiàng)的和為![]() 。
。
(1)求數(shù)列![]() 的首項(xiàng)
的首項(xiàng)![]() 和公比
和公比![]() ;
;
(2)對(duì)給定的![]() ,設(shè)
,設(shè)![]() 是首項(xiàng)為
是首項(xiàng)為![]() ,公差為
,公差為![]() 的等差數(shù)列,求
的等差數(shù)列,求![]() 的前2007項(xiàng)之和;
的前2007項(xiàng)之和;
(3)(理)設(shè)![]() 為數(shù)列
為數(shù)列![]() 的第
的第![]() 項(xiàng),
項(xiàng),![]() :
:
①求![]() 的表達(dá)式,并求出
的表達(dá)式,并求出![]() 取最大值時(shí)
取最大值時(shí)![]() 的值。
的值。
②求正整數(shù)![]() ,使得
,使得![]() 存在且不等于零。
存在且不等于零。
(文)設(shè)![]() 為數(shù)列
為數(shù)列![]() 的第
的第![]() 項(xiàng),
項(xiàng),![]() :求
:求![]() 的表達(dá)式,并求正整數(shù)
的表達(dá)式,并求正整數(shù)![]() ,使得
,使得![]() 存在且不等于零。
存在且不等于零。
定義:若數(shù)列![]() 滿足
滿足![]() ,則稱(chēng)數(shù)列
,則稱(chēng)數(shù)列![]() 為“平方遞推數(shù)列”。已知數(shù)列
為“平方遞推數(shù)列”。已知數(shù)列![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 在函數(shù)
在函數(shù)![]() 的圖像上,其中
的圖像上,其中![]() 為正整數(shù)。
為正整數(shù)。
(1)證明:數(shù)列![]() 是“平方遞推數(shù)列”,且數(shù)列
是“平方遞推數(shù)列”,且數(shù)列![]() 為等比數(shù)列。
為等比數(shù)列。
(2)設(shè)(1)中“平方遞推數(shù)列”的前![]() 項(xiàng)之積為
項(xiàng)之積為![]() ,即
,即![]()
![]() ,求數(shù)列
,求數(shù)列![]() 的通項(xiàng)及
的通項(xiàng)及![]() 關(guān)于
關(guān)于![]() 的表達(dá)式。
的表達(dá)式。
(3)記![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項(xiàng)之和
項(xiàng)之和![]() ,并求使
,并求使![]()
![]() 的
的![]() 的最小值。
的最小值。
1. 學(xué)模擬試卷(2009.3).files/image209.gif) 2.
2. 學(xué)模擬試卷(2009.3).files/image211.gif) 3.
3.學(xué)模擬試卷(2009.3).files/image213.gif) 4.
4.學(xué)模擬試卷(2009.3).files/image215.gif) 5.
5.學(xué)模擬試卷(2009.3).files/image217.gif) 6.(文)
6.(文)學(xué)模擬試卷(2009.3).files/image219.gif) (理)
(理)學(xué)模擬試卷(2009.3).files/image221.gif)
7.學(xué)模擬試卷(2009.3).files/image223.gif) 8. 4 9.(文)
8. 4 9.(文)學(xué)模擬試卷(2009.3).files/image225.gif) (理)1 10.
(理)1 10.學(xué)模擬試卷(2009.3).files/image227.gif) 11.
11.學(xué)模擬試卷(2009.3).files/image229.gif)
12-15. C A A B
16. (1)學(xué)模擬試卷(2009.3).files/image231.gif) .
.
(2)取學(xué)模擬試卷(2009.3).files/image233.gif) 的中點(diǎn)
的中點(diǎn)學(xué)模擬試卷(2009.3).files/image235.gif) ,所求的角的大小等于
,所求的角的大小等于學(xué)模擬試卷(2009.3).files/image237.gif) 的大小,
的大小,
學(xué)模擬試卷(2009.3).files/image239.gif) 中
中學(xué)模擬試卷(2009.3).files/image241.gif) ,所以
,所以學(xué)模擬試卷(2009.3).files/image122.gif) 與底面
與底面學(xué)模擬試卷(2009.3).files/image124.gif) 所成的角的大小是
所成的角的大小是學(xué)模擬試卷(2009.3).files/image243.gif) .
.
17. (1)由函數(shù)學(xué)模擬試卷(2009.3).files/image245.gif) 的圖像與x軸的任意兩個(gè)相鄰交點(diǎn)間的距離為
的圖像與x軸的任意兩個(gè)相鄰交點(diǎn)間的距離為學(xué)模擬試卷(2009.3).files/image247.gif) 得函數(shù)周期為
得函數(shù)周期為學(xué)模擬試卷(2009.3).files/image249.gif) ,
,
學(xué)模擬試卷(2009.3).files/image251.gif)
學(xué)模擬試卷(2009.3).files/image253.gif) 直線
直線學(xué)模擬試卷(2009.3).files/image255.gif) 是函數(shù)
是函數(shù)學(xué)模擬試卷(2009.3).files/image245.gif) 圖像的一條對(duì)稱(chēng)軸,
圖像的一條對(duì)稱(chēng)軸,學(xué)模擬試卷(2009.3).files/image257.gif) ,
,
學(xué)模擬試卷(2009.3).files/image259.gif) 或
或學(xué)模擬試卷(2009.3).files/image261.gif) ,
,學(xué)模擬試卷(2009.3).files/image263.gif) ,
, 學(xué)模擬試卷(2009.3).files/image265.gif) ,
, 學(xué)模擬試卷(2009.3).files/image267.gif) .
. 學(xué)模擬試卷(2009.3).files/image269.gif) .
.
(2)學(xué)模擬試卷(2009.3).files/image271.gif)
學(xué)模擬試卷(2009.3).files/image273.gif)
學(xué)模擬試卷(2009.3).files/image275.gif) ,
,
即函數(shù)學(xué)模擬試卷(2009.3).files/image277.gif) 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為學(xué)模擬試卷(2009.3).files/image279.gif) .
.
18. (1)第學(xué)模擬試卷(2009.3).files/image195.gif) 天銷(xiāo)售的件數(shù)為
天銷(xiāo)售的件數(shù)為學(xué)模擬試卷(2009.3).files/image282.gif)
則學(xué)模擬試卷(2009.3).files/image284.gif)
則:學(xué)模擬試卷(2009.3).files/image286.gif)
解得學(xué)模擬試卷(2009.3).files/image288.gif) ,即
,即
(2)學(xué)模擬試卷(2009.3).files/image288.gif) 時(shí),
時(shí),學(xué)模擬試卷(2009.3).files/image290.gif) ,即未流行
,即未流行
學(xué)模擬試卷(2009.3).files/image292.gif) 時(shí),
時(shí),學(xué)模擬試卷(2009.3).files/image294.gif)
即從
當(dāng)學(xué)模擬試卷(2009.3).files/image296.gif) 時(shí),
時(shí),學(xué)模擬試卷(2009.3).files/image298.gif) ,令
,令學(xué)模擬試卷(2009.3).files/image300.gif) ,解得
,解得學(xué)模擬試卷(2009.3).files/image302.gif)
即從
19. (1)學(xué)模擬試卷(2009.3).files/image304.gif)
(2) 妨設(shè)學(xué)模擬試卷(2009.3).files/image147.gif) 在第一象限,則
在第一象限,則學(xué)模擬試卷(2009.3).files/image307.gif)
學(xué)模擬試卷(2009.3).files/image309.gif)
(3)若直線斜率存在,設(shè)為學(xué)模擬試卷(2009.3).files/image311.gif) ,代入
,代入學(xué)模擬試卷(2009.3).files/image304.gif)
得學(xué)模擬試卷(2009.3).files/image313.gif)
若平行四邊形學(xué)模擬試卷(2009.3).files/image164.gif) 為矩形,則
為矩形,則學(xué)模擬試卷(2009.3).files/image316.gif)
學(xué)模擬試卷(2009.3).files/image318.gif)
學(xué)模擬試卷(2009.3).files/image320.gif)
學(xué)模擬試卷(2009.3).files/image322.gif) 無(wú)解
無(wú)解
若直線垂直學(xué)模擬試卷(2009.3).files/image324.gif) 軸,則
軸,則學(xué)模擬試卷(2009.3).files/image326.gif) 不滿足.
不滿足.
故不存在直線學(xué)模擬試卷(2009.3).files/image155.gif) ,使
,使學(xué)模擬試卷(2009.3).files/image164.gif) 為矩形.
為矩形.
20. 解:(1)由題意的:f ?1(x)=學(xué)模擬試卷(2009.3).files/image330.gif) = f(x)=
= f(x)=學(xué)模擬試卷(2009.3).files/image332.gif) ,所以p = ?1,所以an=
,所以p = ?1,所以an=學(xué)模擬試卷(2009.3).files/image334.gif) 翰林匯
翰林匯
(2) an=學(xué)模擬試卷(2009.3).files/image334.gif) ,dn=
,dn=學(xué)模擬試卷(2009.3).files/image336.gif) =n,
=n,
Sn為數(shù)列{dn}的前n項(xiàng)和,Sn=學(xué)模擬試卷(2009.3).files/image338.gif) ,又Hn為數(shù)列{Sn}的調(diào)和平均數(shù),
,又Hn為數(shù)列{Sn}的調(diào)和平均數(shù),
Hn=學(xué)模擬試卷(2009.3).files/image340.gif) =
=學(xué)模擬試卷(2009.3).files/image342.gif) =
=學(xué)模擬試卷(2009.3).files/image344.gif)
學(xué)模擬試卷(2009.3).files/image201.gif) =
=學(xué)模擬試卷(2009.3).files/image347.gif) =
=學(xué)模擬試卷(2009.3).files/image219.gif)
(3)因?yàn)檎龜?shù)數(shù)列{cn}的前n項(xiàng)之和Tn=學(xué)模擬試卷(2009.3).files/image219.gif) (cn+
(cn+學(xué)模擬試卷(2009.3).files/image351.gif) ),
),
所以c1=學(xué)模擬試卷(2009.3).files/image219.gif) (c1+
(c1+學(xué)模擬試卷(2009.3).files/image353.gif) ),解之得:c1=1,T1=1
),解之得:c1=1,T1=1
當(dāng)n≥2時(shí),cn = Tn?Tn?1,所以2Tn = Tn?Tn?1 +學(xué)模擬試卷(2009.3).files/image355.gif) ,
,
Tn +Tn?1 = 學(xué)模擬試卷(2009.3).files/image355.gif) ,即:
,即:學(xué)模擬試卷(2009.3).files/image358.gif) = n,
= n,
所以,學(xué)模擬試卷(2009.3).files/image360.gif) = n?1,
= n?1,學(xué)模擬試卷(2009.3).files/image362.gif) = n?2,……,
= n?2,……,學(xué)模擬試卷(2009.3).files/image364.gif) =2,累加得:
=2,累加得:
學(xué)模擬試卷(2009.3).files/image366.gif) =2+3+4+……+ n,
=2+3+4+……+ n, 學(xué)模擬試卷(2009.3).files/image368.gif) =1+2+3+4+……+ n =
=1+2+3+4+……+ n =學(xué)模擬試卷(2009.3).files/image370.gif) ,Tn=
,Tn=學(xué)模擬試卷(2009.3).files/image372.gif)
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com