
題目列表(包括答案和解析)
已知圓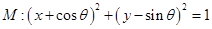 ,直線
,直線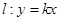 ,給出下列命題:
,給出下列命題: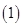 對任意實數
對任意實數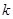 與
與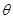 ,直線
,直線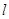 和圓
和圓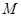 相切;
相切; 對任意實數
對任意實數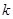 與
與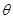 ,直線
,直線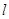 和圓
和圓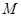 有公共點;
有公共點;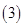 對任意實數
對任意實數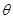 ,必存在實數
,必存在實數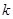 ,使得直線
,使得直線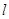 和圓
和圓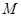 相切;
相切;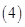 對任意實數
對任意實數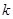 ,必存在實數
,必存在實數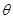 ,使得直線
,使得直線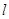 和圓
和圓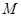 相切;其中正確的是 (填序號)
相切;其中正確的是 (填序號)
已知圓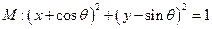 ,直線
,直線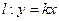 ,給出下列命題:
,給出下列命題: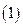 對任意實數
對任意實數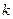 與
與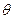 ,直線
,直線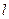 和圓
和圓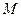 相切;
相切; 對任意實數
對任意實數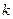 與
與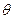 ,直線
,直線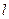 和圓
和圓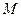 有公共點;
有公共點; 對任意實數
對任意實數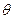 ,必存在實數
,必存在實數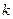 ,使得直線
,使得直線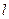 和圓
和圓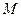 相切;
相切; 對任意實數
對任意實數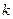 ,必存在實數
,必存在實數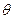 ,使得直線
,使得直線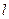 和圓
和圓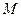 相切;其中正確的是 (填序號)
相切;其中正確的是 (填序號)
已知圓![]() ,直線l:y=kx,下面四個命題:
,直線l:y=kx,下面四個命題:
①對任意實數k與![]() ,直線l和圓M相切;
,直線l和圓M相切;
②對任意實數k與![]() ,直線l和圓M有公共點;
,直線l和圓M有公共點;
③對任意實數![]() ,必存在實數k,使得直線l和圓M相切;
,必存在實數k,使得直線l和圓M相切;
④對任意實數k,必存在實數![]() ,使得直線l和圓M相切、
,使得直線l和圓M相切、
其中真命題的序號是_________.(寫出所有真命題的序號)
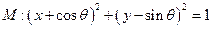 ,直線
,直線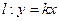 ,給出下列命題:
,給出下列命題: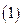 對任意實數
對任意實數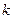 與
與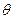 ,直線
,直線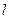 和圓
和圓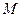 相切;
相切; 對任意實數
對任意實數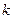 與
與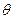 ,直線
,直線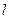 和圓
和圓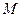 有公共點;
有公共點; 對任意實數
對任意實數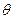 ,必存在實數
,必存在實數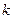 ,使得直線
,使得直線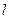 和圓
和圓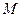 相切;
相切;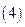 對任意實數
對任意實數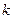 ,必存在實數
,必存在實數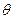 ,使得直線
,使得直線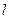 和圓
和圓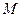 相切;其中正確的是 (填序號)
相切;其中正確的是 (填序號)已知圓M:![]() ,直線l:
,直線l:![]() ,下面四個命題:
,下面四個命題:
A.對任意實數k與q,直線l和圓M相切;
B.對任意實數k與q,直線l和圓M有公共點;
C.對任意實數q,必存在實數k,使得直線l與和圓M相切
D.對任意實數k,必存在實數q,使得直線l與和圓M相切
其中真命題的代號是______________(寫出所有真命題的代號)
一、選擇題(5’×12=60’)
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
C
D
C
D
A
B
A
C
B
A
12.解:令.files/image097.gif) ,則
,則.files/image099.gif) ,由
,由.files/image053.gif) 得
得.files/image101.gif) ,
,
∴點B所在的區域是以點.files/image103.gif) 為頂點的三角形,其面積
為頂點的三角形,其面積.files/image105.gif) .故選A.
.故選A.
13.x2+y2=4
14.12.files/image107.gif) 15.
15..files/image109.gif)
16.②④
17.(12分)求與直線3x-4y+7=0平行且在兩坐標軸上的截距之和為1的直線方程.
17.解:設所求直線方程為3x-4y+m=0,
令x=0,得y=.files/image111.gif) ;令
;令.files/image113.gif) 得
得.files/image115.gif) .
.
依題意得.files/image117.gif)
∴所求的直線方程為3x-4y-12=0.
18.(12分)直線y=2x與拋物線y=-x2-2x+m相交于不同的兩點A、B,求
(1)實數m的取值范圍;(2)ㄏABㄏ的值(用含m的代數式表示).
18.將y=2x代入y=-x2-2x+m得,x2+4x-m=0.
∵直線與拋物線相交于不同的兩點A、B,∴.files/image119.gif)
(2)設.files/image121.gif) ,則
,則
ㄏABㄏ=.files/image123.gif) .
.
19.(本小題滿分12分)(理)如圖,已知矩形ABCD,PA⊥平面ABCD,M、N分別是AB、PC的中點,設AB=a,BC=b,PA=c.
(1)證明MN⊥AB;
|