
題目列表(包括答案和解析)
| x-2 |
| x2 |
| x |
| 1 |
| 2 |
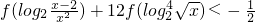 .
.| x-2 |
| x2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| x+y |
| 1+xy |
| 1 |
| 2 |
| 2a | ||
1+
|
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| f(a1) |
| 1 |
| f(a2) |
| 1 |
| f(a3) |
| 1 |
| f(an) |
| 6 |
| 7 |
| g | 2 2 |
| 18 |
| 7 |
| 1 |
| 2 |
| x+y |
| 1+xy |
| 1 |
| 2 |
| 2a | ||
1+
|
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| f(a1) |
| 1 |
| f(a2) |
| 1 |
| f(a3) |
| 1 |
| f(an) |
| 6 |
| 7 |
| g | 22 |
| 18 |
| 7 |
一、選擇題:
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
A
C
D
C
C
A
D
B
D
C
二、填空題(本大題共4小題,每小題4分,共16分)
13、理科數學.files/image202.gif) ; 14、
; 14、理科數學.files/image204.gif) ; 15、32; 16、2
; 15、32; 16、2
三、解答題:(本大題共6小題,共74分,)
17、解:(I)理科數學.files/image133.gif)
理科數學.files/image206.gif)
理科數學.files/image208.gif) ……………………………………………………4分
……………………………………………………4分
理科數學.files/image210.gif) ………………………………………………………………6分
………………………………………………………………6分
(II)由余弦定理理科數學.files/image212.gif) 得
得
理科數學.files/image214.gif)
理科數學.files/image216.gif) ……………………………………………………………………9分
……………………………………………………………………9分
而理科數學.files/image218.gif) ,
,理科數學.files/image220.gif)
函數理科數學.files/image222.gif)
當理科數學.files/image224.gif) ………………………………………12分
………………………………………12分
18、解:由上表可求出10次記錄下的有記號的紅鯽魚與中國金魚數目的平均數均為20,故可認為池塘中的紅鯽魚與中國金魚的數目相同,設池塘中兩種魚的總數是理科數學.files/image050.gif) ,則有
,則有
理科數學.files/image227.gif) , 即
, 即 理科數學.files/image229.gif) ,
------------4分
,
------------4分
所以,可估計水庫中的紅鯽魚與中國金魚的數量均為25000. ------------6分
(Ⅱ)顯然,理科數學.files/image231.gif) ,
-----------9分
,
-----------9分
其分布列為
理科數學.files/image146.gif)
0
1
2
3
4
5
理科數學.files/image233.gif)
理科數學.files/image235.gif)
理科數學.files/image237.gif)
理科數學.files/image239.gif)
理科數學.files/image239.gif)
理科數學.files/image237.gif)
理科數學.files/image235.gif)
---------11分
數學期望理科數學.files/image242.gif) .
-----------12分
.
-----------12分
|