
B.
C.
D.
2.已知 ,在下列各小題中,M是N的充分不必要條件的是( )
,在下列各小題中,M是N的充分不必要條件的是( )
A.M: ,N:
,N: B.M:
B.M: ,N:
,N:
C.M: , N:
, N: D.M:
D.M: , N:
, N:
3.不等式 的解集為
的解集為 ,則函數
,則函數

 的圖象為(
)
的圖象為(
)
4.已知等差數列 和等比數列
和等比數列 ,對任意
,對任意 都有
都有 ,且
,且 ,那么
,那么 的大小關系是( )
的大小關系是( )
A.  B.
B.  C.
C.  D.
D. 
 5.如圖,在正方體
5.如圖,在正方體 中,P是側面
中,P是側面 內一動點,若
內一動點,若
P到平面 的距離是P到直線
的距離是P到直線 的距離的
的距離的 ,
,
則動點P的軌跡所在的曲線是( )
A. 直線 B. 橢圓 C. 雙曲線 D. 拋物線
6. 設m、n是不同的直線,α、β、γ是不同的平面,有以下四個命題:
① ;②
;② ;③
;③ ;
;
④ ,其中為真命題的是( )
,其中為真命題的是( )
A.①②
B.②③
C.①③
D.③④
7.當 滿足條件
滿足條件 (
( 為常數)時,能使
為常數)時,能使 的最大值為12的
的最大值為12的 的值( )
的值( )
A.-9 B.9
C.-12 D.12
8.據有關資料表明,世界人口由1976年的40億增加到1987年的50億,
經歷了11年的時間,如果按此增長率增長,2020年的世界人口數將接近
( )
A.88億
B. 98億
C. 108億 D.
118億
9.已知定點 .若動點P在拋物線
.若動點P在拋物線 上,且點P在
上,且點P在 軸上的射影為點M,則
軸上的射影為點M,則 的最大值是( )
的最大值是( )
A.5 B. C. 4 D. 3
C. 4 D. 3
10.設函數 ,若關于
,若關于 的方程
的方程
 恰有3個不同的實數解
恰有3個不同的實數解 ,
,
則 等于( )
等于( )
A.0
B.lg2
C.lg4 D.l
二.填寫題:本大題共6小題,每小題4分,共24分 把答案填在答題卡相應位置
把答案填在答題卡相應位置
11.設 ,若
,若 ,則
,則 的值為 .
的值為 .
12. 以點(1,2)為圓心,與直線 相切的圓的方程
相切的圓的方程
為
.
13.某地球儀上北緯 緯線的長度為
緯線的長度為 ,該地球儀表面積
,該地球儀表面積
是
cm2.
14.若 展開式中含
展開式中含 的項的系數等于含
的項的系數等于含 的項的系數的8倍,則
的項的系數的8倍,則 等于 .
等于 .
15.設平面內的兩個向量 互相垂直,且
互相垂直,且 ,又
,又 與
與
是兩個不同時為零的實數,若向量 與
與 互相垂直,則
互相垂直,則 的最大值為
.
的最大值為
.
16. 將A,B,C,D,E五種不同的文件放入一排編號依次為1,2,3,4,5,6的六個抽屜內,每個抽屜至多放一種文件.若文件A,B必須放入相鄰的抽屜內,文件D,E必須放入不相鄰的抽屜內,則滿足條件的所有不同放法有 .
三.解答題:本大題共5小題,共70分 解答應寫出文字說明.證明過程或演算步驟
解答應寫出文字說明.證明過程或演算步驟
17.(本小題滿分13分)
一位射擊選手以往1000次的射擊結果統計如下表(設所打環數均為整數):
環數
10
9
8
7
6
5
頻數
250
350
200
130
50
20
試根據以上統計數據估算:
(1)該選手一次射擊打出的環數不低于8環的概率;
(2)估算該選手他射擊4次至多有兩次不低于8環的概率;
(3)在一次比賽中,該選手的發揮超出了按上表統計的平均水平.若已知他在10次射擊中,每一次的環數都不小于6,且其中有6環、8環各1個,2個7環,試確定該選手在這次比賽中至少打出了多少個10環?
 18.(本小題滿分13分)
18.(本小題滿分13分)
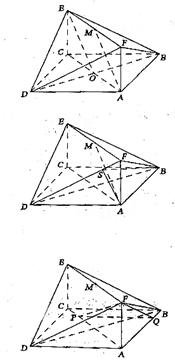
如圖,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是線段EF的中點.
,AF=1,M是線段EF的中點.
(1)求證AM//平面BDE;
(2)求二面角A-DF-B的大小;
(3)試在線段AC上確定一點P,使得PF與BC所成的角是60°.
19.(本小題滿分14分)
飛船返回倉順利到達地球后,為了及時將航天員救出,地面指揮中心在返回倉預計到達區域安排三個救援中心(記為A,B,C),B在A的正東方向,相距6km,C在B的北偏東300,相距4km,P為航天員著陸點,某一時刻A接到P的求救信號,由于B、C兩地比A距P遠,因此4s后,B、C兩個救援中心才同時接收到這一信號,已知該信號的傳播速度為1km/s.
(1)求A、C兩個救援中心的距離;
(2)求在A處發現P的方向角;
 (3)若信號從P點的正上方Q點處發出,則A、B收到信號的時間差變大還是變小,并證明你的結論.
(3)若信號從P點的正上方Q點處發出,則A、B收到信號的時間差變大還是變小,并證明你的結論.
20.(本小題滿分15分)
已知數列 .
.
設 ,
, 為數列{
為數列{ }的前
}的前 項和.
項和.
(1)求證:{ }為等比數列;
}為等比數列;
(2)當 時,求
時,求 ;
;
(3)當 時,是否存在正整數
時,是否存在正整數 ,使得對于任意正整數
,使得對于任意正整數 都有
都有 ?如果存在,求出
?如果存在,求出 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
21.(本小題滿分15分)
對于函數 ,若存在
,若存在 使
使 成立,則稱
成立,則稱 是
是 的不動點. 已知函數
的不動點. 已知函數 ,
,
(1)當 時,求
時,求 的不動點;
的不動點;
(2)若規定 ,…,
,…, ,
, 為大于1的正整數.
為大于1的正整數.
①證明:若函數 無不動點時,則函數
無不動點時,則函數 也無不動點;
也無不動點;
②證明:若函數 存在唯一不動點,則函數
存在唯一不動點,則函數 也存在唯一不動點.
也存在唯一不動點.
高三數學答題紙
一選擇題:(每小題5分)
1
2
3
4
5
6
7
8
9
10
二、填空題:(每小題5分)
試題詳情
試題詳情
試題詳情
三.解答題:
試題詳情
試題詳情
試題詳情
 19.
19.
試題詳情
試題詳情
高三數學答案 2006.4
一選擇題:(每小題5分)
1
2
3
4
5
6
7
8
9
10
D
B
C
D
C
C
A
B
A
C
試題詳情
二、填空題:(每小題5分)
試題詳情
試題詳情
三.解答題:
17.解:(1) 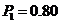
試題詳情
(2)
試題詳情
故所求為1-0.4096-0.4096=0.1808
(3)設這次比賽中該選手打出了m個9環,n個10環
試題詳情
試題詳情
又m+n=6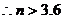 ,故在此次比賽中該選手至少打出了4個10環 .
,故在此次比賽中該選手至少打出了4個10環 .
試題詳情
 18.方法一
18.方法一
解: (1)記AC與BD的交點為O,連接OE,
∵O、M分別是AC、EF的中點,ACEF是矩形,
∴四邊形AOEM是平行四邊形,∴AM∥OE。
試題詳情
∵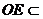 平面BDE,
平面BDE,
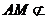 平面BDE,∴AM∥平面BDE。
平面BDE,∴AM∥平面BDE。
(2)在平面AFD中過A作AS⊥DF于S,連結BS,
試題詳情
∵AB⊥AF, AB⊥AD, 
∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
由三垂線定理得BS⊥DF。
∴∠BSA是二面角A―DF―B的平面角。
試題詳情
在RtΔASB中,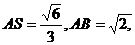 ∴
∴
∴二面角A―DF―B的大小為60º。
(3)設CP=t(0≤t≤2),作PQ⊥AB于Q,則PQ∥AD,
試題詳情
∵PQ⊥AB,PQ⊥AF, ,
,
試題詳情
∴PQ⊥平面ABF,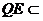 平面ABF,∴PQ⊥QF。
平面ABF,∴PQ⊥QF。
在RtΔPQF中,∠FPQ=60º,PF=2PQ。
試題詳情
∵ΔPAQ為等腰直角三角形,∴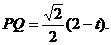 又∵ΔPAF為直角三角形,
又∵ΔPAF為直角三角形,
試題詳情
∴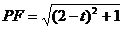 , ∴
, ∴
所以t=1或t=3(舍去)即點P是AC的中點。
方法二 :(1)建立如圖所示的空間直角坐標系。
試題詳情
試題詳情
試題詳情
又∵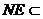 平面BDE,
平面BDE, 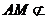 平面BDE,∴AM∥平面BDF。
平面BDE,∴AM∥平面BDF。
試題詳情
(2)∵AF⊥AB,AB⊥AD,AF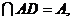 ∴AB⊥平面ADF。
∴AB⊥平面ADF。
試題詳情
∴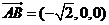 為平面DAF的法向量。
為平面DAF的法向量。
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
(3)設P(t,t,0)(0≤t≤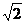 )得
)得
試題詳情
試題詳情
試題詳情
19. 解:(1)以AB中點為坐標原點,AB所在直線為x軸建立平面直角坐標系,則
試題詳情
試題詳情
則
試題詳情
即A、C兩個救援中心的距離為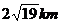
試題詳情
(2)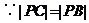 ,所以P在BC線段的垂直平分線上
,所以P在BC線段的垂直平分線上
試題詳情
試題詳情
∴雙曲線方程為
試題詳情
BC的垂直平分線的方程為
試題詳情
聯立兩方程解得:
試題詳情

∴∠PAB=120°所以P點在A點的北偏西30°處
試題詳情
試題詳情
試題詳情
又∵
試題詳情

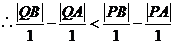 即A、B收到信號的時間差變小
即A、B收到信號的時間差變小
試題詳情
21.證明:(1)當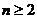 時,
時, ,
,
試題詳情
試題詳情
(2)因為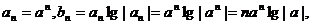
試題詳情
當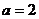 時,
時,
試題詳情
試題詳情
兩式相減,整理得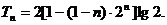
試題詳情
(3)因為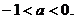 所以,當n為偶數時,
所以,當n為偶數時, ;當n為奇數時,
;當n為奇數時,
試題詳情
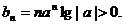 所以,如果存在滿足條件的正整數m,則m一定是偶數.
所以,如果存在滿足條件的正整數m,則m一定是偶數.
試題詳情
試題詳情
試題詳情
試題詳情
試題詳情
即存在正整數m=8,使得對于任意正整數n都有
試題詳情
試題詳情
試題詳情
試題詳情
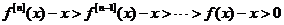 即
即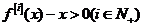 .
.
試題詳情
故函數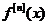 也無不動點.
也無不動點.
試題詳情
試題詳情
試題詳情
下面證明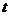 是
是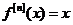 的唯一根.
的唯一根.
試題詳情
由(2)的方法可得
試題詳情
試題詳情
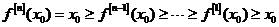 ,
,
試題詳情
試題詳情

 在每小題給出的四個選項中,只有一項是符合題意要求的
在每小題給出的四個選項中,只有一項是符合題意要求的
 都是I的
都是I的