
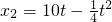 米.
米.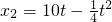 米與勻變速運動的位移公式x=v0t+
米與勻變速運動的位移公式x=v0t+ 對比,得到汽車的初速度v0=10m/s,加速度a=-0.5m/s2.
對比,得到汽車的初速度v0=10m/s,加速度a=-0.5m/s2. t2
t2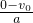 =
=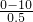 s=20s
s=20s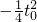 )-v1t0=16m.
)-v1t0=16m.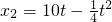 米與勻變速運動的位移公式x=v0t+
米與勻變速運動的位移公式x=v0t+ 對比,得到汽車的加速度和初速度.
對比,得到汽車的加速度和初速度.

 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中物理 來源: 題型:
| 1 | 4 |
查看答案和解析>>
科目:高中物理 來源: 題型:
查看答案和解析>>
科目:高中物理 來源: 題型:
查看答案和解析>>
科目:高中物理 來源:同步題 題型:計算題
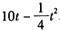 。
。查看答案和解析>>
科目:高中物理 來源:2011-2012學年江蘇省常州中學高一(上)第一次段考物理試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com