
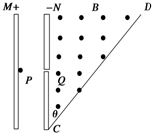
 如圖所示,M、N為兩塊帶等量異種電荷的平行金屬板,兩板間電壓可取從零到最大值Um之間的各種數值.靜止的帶電粒子電荷量為+q,質量為m(不計重力),從點P經電場加速后,從小孔Q進入N板右側的勻強磁場區域,磁場方向垂直于紙面向外,CD為磁場邊界上的一絕緣板,它與N板的夾角為θ=45°,孔Q到板的下端C的距離為L,當M、N兩板間電壓取最大值Um時,粒子恰垂直打在CD板上.求:
如圖所示,M、N為兩塊帶等量異種電荷的平行金屬板,兩板間電壓可取從零到最大值Um之間的各種數值.靜止的帶電粒子電荷量為+q,質量為m(不計重力),從點P經電場加速后,從小孔Q進入N板右側的勻強磁場區域,磁場方向垂直于紙面向外,CD為磁場邊界上的一絕緣板,它與N板的夾角為θ=45°,孔Q到板的下端C的距離為L,當M、N兩板間電壓取最大值Um時,粒子恰垂直打在CD板上.求:分析 帶電粒子在帶等量異種電荷的電場在加速,離開電場進入勻強磁場做勻速圓周運動,由于進入磁場的速度不同,半徑也不相等,本題涉及的幾種特殊情況.
(1)由動能定理,電場力做的功就是粒子動能的增加量,從而求出速度的射入磁場的速度.
(2)由垂直打在板上知道速度方向,從而求出半徑,由洛侖茲力提供向心力就可求出此種情況下磁感應強度的大小.
(3)顯然在磁場中做完整的半周的時間就是最長時間.
(4)由分析知:最大速度的位置打在CD板上離C點最遠,與CD相切的位置最近.兩者之差就是打在CD板上的長度.
解答 解:(1)M、N兩板間電壓取最大值Um時,粒子恰垂直打在CD板上,所以圓心在C點,如圖所示,設此時粒子
運動軌跡半徑為r1,CH=QC=L 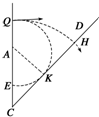
即半徑r1=L
由qUm=$\frac{1}{2}m{{v}_{1}}^{2}$ ${v}_{1}=\sqrt{\frac{2q{U}_{m}}{m}}$
(2)又因為qv1B=m $\frac{{{v}_{1}}^{2}}{{r}_{1}}$
得B=$\sqrt{\frac{2m{U}_{m}}{q{L}^{2}}}$
(3)打在QE間的粒子在磁場中運動的時間最長,均為半個周期,
由$T=\frac{2πr}{v}=\frac{2πm}{qB}$而 ${t}_{m}=\frac{T}{2}$
得tm=$πL\sqrt{\frac{m}{2q{U}_{m}}}$
(4)設粒子在磁場中運動的軌跡與CD板相切于K點,此軌跡的半徑為r2,設圓心為A,在△AKC中:sin 45°=$\frac{{r}_{2}}{L-{r}_{2}}$
解得r2=($\sqrt{2}$-1)L,
由幾何關系:KC=r2=($\sqrt{2}$-1)L
所以CD板上可能被粒子打中的區域的長度s=HK=HC-KC,
即s=r1-r2=(2-$\sqrt{2}$)L
答:(1)當M、N兩板間電壓取最大值Um時,粒子射入磁場的速度v1的大小$\sqrt{\frac{2q{U}_{m}}{m}}$.
(2)勻強磁場的磁感應強度B的大小$\sqrt{\frac{2m{U}_{m}}{q{L}^{2}}}$.
(3)粒子在磁場中運動的最長時間為$πL\sqrt{\frac{m}{2q{U}_{m}}}$
(4)CD板上可能被粒子打中區域的長度S 為(2-$\sqrt{2}$)L.
點評 由洛侖茲力提供向心力可求得半徑公式,從半徑公式可以看出速度越大,半徑越大,打的位置越上,由題意,找到幾種特殊情況,從而能夠求出速度、磁感應強度、最長時間等.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中物理 來源: 題型:解答題
 如圖所示,一長木板置于粗糙水平地面上,木板左端放置一小物塊,木板的質量4kg,小物塊質量1kg,可視為質點;小物塊與木板間的動摩擦因數μ1=0.6,木板與地面間的動摩擦因數μ2=0.1,g=10m/s2;現對小物塊施加水平推力F
如圖所示,一長木板置于粗糙水平地面上,木板左端放置一小物塊,木板的質量4kg,小物塊質量1kg,可視為質點;小物塊與木板間的動摩擦因數μ1=0.6,木板與地面間的動摩擦因數μ2=0.1,g=10m/s2;現對小物塊施加水平推力F查看答案和解析>>
科目:高中物理 來源: 題型:解答題
 如圖所示,在平面坐標系xOy中,x≤0區域有垂直于y軸的勻強電場E=0.4N/C,x>0有三個區域Ⅰ、Ⅱ、Ⅲ,區域邊界垂直于x軸,區域I的寬度L1=0.05m,區域Ⅱ的寬度L2=0.1m,區域Ⅲ的寬度L3未知,三個區域都有勻強磁場,磁感應強度大小相等都為B=0.02T,Ⅰ、Ⅲ中磁場方向垂直于坐標平面向外,Ⅱ中磁場方向垂直于坐標平面向里;P點在y軸上,縱坐標yP=0.15m,A點與P點縱坐標相等,與P點的距離d=1.0m.一正點電荷從A點由靜止開始運動經過P點進入區域I,并從區域Ⅱ、Ⅲ之間邊界上的C點(圖中未標出)進入區域Ⅲ.點電荷質量m=2×10-9kg,電荷量q=4×10-4C,不計重力.
如圖所示,在平面坐標系xOy中,x≤0區域有垂直于y軸的勻強電場E=0.4N/C,x>0有三個區域Ⅰ、Ⅱ、Ⅲ,區域邊界垂直于x軸,區域I的寬度L1=0.05m,區域Ⅱ的寬度L2=0.1m,區域Ⅲ的寬度L3未知,三個區域都有勻強磁場,磁感應強度大小相等都為B=0.02T,Ⅰ、Ⅲ中磁場方向垂直于坐標平面向外,Ⅱ中磁場方向垂直于坐標平面向里;P點在y軸上,縱坐標yP=0.15m,A點與P點縱坐標相等,與P點的距離d=1.0m.一正點電荷從A點由靜止開始運動經過P點進入區域I,并從區域Ⅱ、Ⅲ之間邊界上的C點(圖中未標出)進入區域Ⅲ.點電荷質量m=2×10-9kg,電荷量q=4×10-4C,不計重力.查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
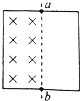 如圖所示,用均勻導線做成邊長為1m的正方形線框,線框的一半處于垂直線框向里的有界勻強磁場中,當磁場以0.2T/s的變化率增強時,a、b兩點的電勢分別為φa、φb,回路中電動勢為E,則( )
如圖所示,用均勻導線做成邊長為1m的正方形線框,線框的一半處于垂直線框向里的有界勻強磁場中,當磁場以0.2T/s的變化率增強時,a、b兩點的電勢分別為φa、φb,回路中電動勢為E,則( )| A. | φa<φb,E=0.2V | B. | φa>φb,E=0.2V | C. | φa<φb,E=0.1V | D. | φa>φb,E=0.1V |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
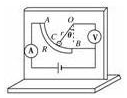 某同學設計了一個測定列車加速度的儀器,如圖所示.AB是一段四分之一圓弧形的電阻,O點為其圓心,且在B點正上方,圓弧半徑為r.O點下用一電阻不計的金屬線懸掛著一個金屬球,球的下部恰好與AB良好接觸且無摩.A、B之間接有內阻不計、電動勢為9V的電池,電路中接有理想電流表A,O、B間接有一個理想電壓表V.整個裝置在一豎直平面內,且裝置所在平面與列車前進的方向平行.下列說法中正確的有( )
某同學設計了一個測定列車加速度的儀器,如圖所示.AB是一段四分之一圓弧形的電阻,O點為其圓心,且在B點正上方,圓弧半徑為r.O點下用一電阻不計的金屬線懸掛著一個金屬球,球的下部恰好與AB良好接觸且無摩.A、B之間接有內阻不計、電動勢為9V的電池,電路中接有理想電流表A,O、B間接有一個理想電壓表V.整個裝置在一豎直平面內,且裝置所在平面與列車前進的方向平行.下列說法中正確的有( )| A. | 從圖中看到列車可能是向左減速運動 | |
| B. | 當列車的加速度增大時,電流表A的讀數增大,電壓表V的讀數也增大 | |
| C. | 若電壓表顯示3 V,則列車的加速度為$\frac{\sqrt{3}}{3}$g | |
| D. | 如果根據電壓表示數與列車加速度的一一對應關系將電壓表改制成一個加速度表,則加速度表的刻度是不均勻的 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
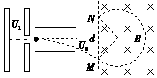 如圖7所示,某種帶電粒子由靜止開始經電壓為U1的電場加速后,射入水平放置、電勢差為U2的兩塊導體板間的勻強電場中,帶電粒子沿平行于兩板的方向從兩板正中間射入,穿過兩板后又垂直于磁場方向射入邊界線豎直的勻強磁場中,則粒子射入磁場和射出磁場的M、N兩點間的距離d隨著U1或U2的變化情況為(不計重力,不考慮邊緣效應)( )
如圖7所示,某種帶電粒子由靜止開始經電壓為U1的電場加速后,射入水平放置、電勢差為U2的兩塊導體板間的勻強電場中,帶電粒子沿平行于兩板的方向從兩板正中間射入,穿過兩板后又垂直于磁場方向射入邊界線豎直的勻強磁場中,則粒子射入磁場和射出磁場的M、N兩點間的距離d隨著U1或U2的變化情況為(不計重力,不考慮邊緣效應)( )| A. | d與U1無關,d隨U2增大而增大 | B. | d與U2無關,d隨U1增大而增大 | ||
| C. | d與U1無關,d隨U2增大而減小 | D. | d與U2無關,d隨U1增大而減小 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
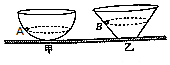 如圖所示,甲表示小球A在半球形容器中做勻速圓周運動,乙表示小球B在一個圓錐形容器中做勻速圓周運動.不考慮兩球在運動過程中的阻力.如果A、B的線速度均增大,下列關于兩球運動角速度的說法正確的是( )
如圖所示,甲表示小球A在半球形容器中做勻速圓周運動,乙表示小球B在一個圓錐形容器中做勻速圓周運動.不考慮兩球在運動過程中的阻力.如果A、B的線速度均增大,下列關于兩球運動角速度的說法正確的是( )| A. | A的增大、B的也增大 | B. | A的增大、B的減小 | ||
| C. | A的減小、B的增大 | D. | A的減小、B的也減小 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
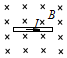 如圖所示,一通電直導線位于勻強磁場中,導線與磁場方向垂直.當導線中的電流為I時,通電導線所受安培力的大小為F.當該導線中的電流變為2I時,保持其他條件不變,通電導線所受安培力的大小為( )
如圖所示,一通電直導線位于勻強磁場中,導線與磁場方向垂直.當導線中的電流為I時,通電導線所受安培力的大小為F.當該導線中的電流變為2I時,保持其他條件不變,通電導線所受安培力的大小為( )| A. | $\frac{F}{2}$ | B. | F | C. | 2F | D. | 4F |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com