
分析 同步衛星總是在赤道上空,其高度也是一定的.由它畫一條到地球表面的切線,可見兩極周圍的區域內就收不到微波通訊.
根據萬有引力提供向心力和數學幾何關系求解.根據幾何關系求出極地衛星的軌道半徑,由萬有引力提供向心力即可求出極地衛星的周期.
解答  解:以m、M分別表示同步衛星和地球的質量,r表示同步衛星到地心的距離,T表示地球的自轉周期,則
解:以m、M分別表示同步衛星和地球的質量,r表示同步衛星到地心的距離,T表示地球的自轉周期,則
$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
地球表面萬有引力等于重力$G\frac{Mm}{{R}_{0}^{2}}=mg$
根據幾何關系:$rsinα={R}_{0}^{\;}$
對于極地衛星,軌道半徑為r′,周期為T′
$r′cosα={R}_{0}^{\;}$
有$G\frac{Mm}{r{′}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{T{′}_{\;}^{2}}r′$
得$T′=\sqrt{\frac{r{′}_{\;}^{3}}{{r}_{\;}^{3}}}T$=$(\frac{{R}_{0}^{\;}}{\sqrt{(\frac{g{R}_{0}^{2}{T}_{\;}^{2}}{4{π}_{\;}^{2}})}-{R}_{0}^{2}})^{\frac{3}{2}}T$
答:這顆極地衛星繞地球的周期至少為$(\frac{{R}_{0}^{\;}}{\sqrt{(\frac{g{R}_{0}^{2}{T}_{\;}^{2}}{4{π}_{\;}^{2}})}-{R}_{0}^{2}})^{\frac{3}{2}}T$
點評 解決該題關鍵要根據題意找出收不到微波區域的面積,善于把物理問題與數學幾何圖形結合運用


科目:高中物理 來源: 題型:計算題
查看答案和解析>>
科目:高中物理 來源: 題型:實驗題
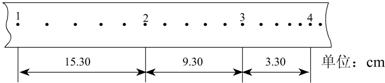
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | UI | B. | UI-I2R | C. | UI+I2R | D. | $\frac{{U}^{2}}{R}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | M=$\frac{{4{π^2}{{(R+h)}^3}}}{{G{T^2}}}$ | B. | M=$\frac{(R+h)^{2}g}{G}$ | C. | M=$\frac{{4{π^2}{R^3}}}{{G{T^2}}}$ | D. | M=$\frac{4{π}^{2}{h}^{3}}{G{T}^{2}}$ |
查看答案和解析>>
科目:高中物理 來源: 題型:計算題
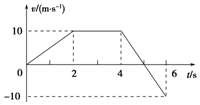 一物體自t=0時開始做直線運動,其速度圖線如圖所示,求:
一物體自t=0時開始做直線運動,其速度圖線如圖所示,求:查看答案和解析>>
科目:高中物理 來源: 題型:選擇題

| A. | 電勢ΦA<ΦB,場強EA<EB | |
| B. | 電勢ΦA>ΦB,場強EA>EB | |
| C. | 將+q電荷從A點移動到B點電場力做正功 | |
| D. | 將-q電荷分別放在A、B兩點時具有的電勢能EPA>EPB |
查看答案和解析>>
科目:高中物理 來源: 題型:多選題
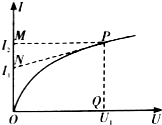 某電子元件通電后其電流I隨所加電壓U變化的圖線如圖所示,P為圖線上一點,PN為圖線的切線,PQ為U軸的垂線,PM為I軸的垂線,下列說法中正確的是( )
某電子元件通電后其電流I隨所加電壓U變化的圖線如圖所示,P為圖線上一點,PN為圖線的切線,PQ為U軸的垂線,PM為I軸的垂線,下列說法中正確的是( )| A. | 隨著所加電壓的增大,該元件的電阻增大 | |
| B. | 對應P點,該元件的電阻為R=$\frac{{U}_{1}}{{I}_{1}}$ | |
| C. | 對應P點,該元件的電阻為R=$\frac{{U}_{1}}{{I}_{2}-{I}_{1}}$ | |
| D. | 該元件為非線性元件 |
查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
| A. | 該定義只適用于點電荷產生的電場 | |
| B. | 庫侖定律的表達式F=k$\frac{{q}_{1}{q}_{2}}{{r}^{2}}$可以說是點電荷q2產生的電場在點電荷q1處的庫侖力大小;而k$\frac{{q}_{1}}{{r}^{2}}$可以說是點電荷q2產生的電場在點電荷q1處的場強大小 | |
| C. | 對E=$\frac{F}{q}$,F是放入電場中的點電荷所受的靜電力,q是產生電場的電荷的電荷量 | |
| D. | 電場中某點場強的方向與試探電荷的正負無關 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com