
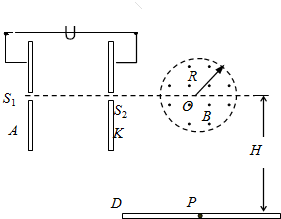
 如圖,在以O為圓心、半徑R═10$\sqrt{3}$cm的圓形區域內,有一個方向垂直于紙面向外的水平勻強磁場.磁感應強度B=0.1T,兩金屬極板A、K豎直平行放置,A、K間的電壓U=900V,S1、S2為A、K板上的兩個小孔,且S1、S2跟O處于垂直極板的同一水平線上,在O點下方距離O點H=3R處有一塊足夠長的熒光屏D放置在水平面內,比荷為$\frac{q}{m}$=2.0×106C/kg的離子流由S1進入電場后,之后沿S2、O連線離開電場并隨后射入磁場,通過磁場后落到熒光屏上.離子進入電場的初速度、離子的重力,離子之間的相互作用力均可忽略不計.
如圖,在以O為圓心、半徑R═10$\sqrt{3}$cm的圓形區域內,有一個方向垂直于紙面向外的水平勻強磁場.磁感應強度B=0.1T,兩金屬極板A、K豎直平行放置,A、K間的電壓U=900V,S1、S2為A、K板上的兩個小孔,且S1、S2跟O處于垂直極板的同一水平線上,在O點下方距離O點H=3R處有一塊足夠長的熒光屏D放置在水平面內,比荷為$\frac{q}{m}$=2.0×106C/kg的離子流由S1進入電場后,之后沿S2、O連線離開電場并隨后射入磁場,通過磁場后落到熒光屏上.離子進入電場的初速度、離子的重力,離子之間的相互作用力均可忽略不計.分析 (1)粒子要能落到熒光屏上,說明洛倫茲力的方向向下,根據左手定則判斷粒子的電性;
(2)根據動能定理求出粒子進入磁場的速度,進入磁場后做勻速圓周運動,求出在磁場中做圓周運動的半徑,根據幾何關系求出圓弧所對的圓心角,由幾何關系即可求出離子到達光屏時的位置與P點的距離
解答 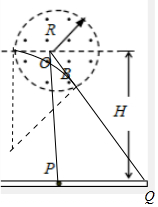 解:(1)離子在AK間加速,受向右的電場力,進入磁場后,離子落到熒光屏上,說明洛倫茲力向下,根據左手定則判斷離子帶正電;
解:(1)離子在AK間加速,受向右的電場力,進入磁場后,離子落到熒光屏上,說明洛倫茲力向下,根據左手定則判斷離子帶正電;
(2)離子通過電場過程,根據動能定理:
$qU=\frac{1}{2}m{v}_{\;}^{2}-0$
解得:$v=\sqrt{\frac{2qU}{m}}=\sqrt{2×2.0×1{0}_{\;}^{6}×900}$=$6×1{0}_{\;}^{4}m/s$
離子進入磁場后做勻速圓周運動,洛倫茲力提供向心力,有
$qvB=m\frac{{v}_{\;}^{2}}{r}$
解得:$r=\frac{mv}{qB}=\frac{6×1{0}_{\;}^{4}}{2.0×1{0}_{\;}^{6}×0.1}=0.3m=30cm$
軌跡圓弧所對的圓心角為θ,$tan\frac{θ}{2}=\frac{R}{r}=\frac{10\sqrt{3}}{30}=\frac{\sqrt{3}}{3}$
解得:θ=60°
根據幾何關系,∠POQ=30°
設離子到達熒光屏上的Q點
$tan30°=\frac{PQ}{H}$
解得:$PQ=\frac{\sqrt{3}}{3}H=\frac{\sqrt{3}}{3}×3R=\sqrt{3}×10\sqrt{3}=30cm$
答:(1)指出離子的電性帶正電
(2)離子到達光屏時的位置與P點的距離為30cm
點評 本題分析離子的運動情況是求解的關鍵和基礎,考查綜合應用電路、磁場和幾何知識,處理帶電粒子在復合場中運動問題的能力,綜合性較強.


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中物理 來源: 題型:填空題
查看答案和解析>>
科目:高中物理 來源: 題型:解答題
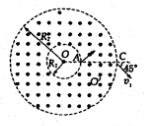 如圖所示,在以O為圓心,內外半徑分別為R1和R2的圓環區域內,存在垂直紙面的勻強磁場,R1=R0,R2=3R0,一電荷量為+q,質量為m的粒子從內圓上的A點進入該區域,不計重力.
如圖所示,在以O為圓心,內外半徑分別為R1和R2的圓環區域內,存在垂直紙面的勻強磁場,R1=R0,R2=3R0,一電荷量為+q,質量為m的粒子從內圓上的A點進入該區域,不計重力.查看答案和解析>>
科目:高中物理 來源: 題型:解答題
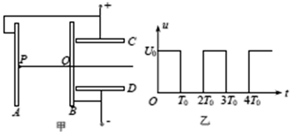 如圖甲所示,兩組平行正對金屬板A、B和C、D,C、D的左端緊靠B板,A與C、B與D分別連接后,接上如圖乙所示規律變化的電壓,忽略極板正對部分之外的電場.位于A板中心P處的粒子源可以產生比荷($\frac{q}{m}$)為k的帶正電粒子,粒子的重力和初速度均可忽略不計.已知t=0時刻產生的粒子,恰好在t=2T0時刻從B板中心的小孔Q處穿過,并在t=3T0時刻緊貼D板的右邊緣離開,求:
如圖甲所示,兩組平行正對金屬板A、B和C、D,C、D的左端緊靠B板,A與C、B與D分別連接后,接上如圖乙所示規律變化的電壓,忽略極板正對部分之外的電場.位于A板中心P處的粒子源可以產生比荷($\frac{q}{m}$)為k的帶正電粒子,粒子的重力和初速度均可忽略不計.已知t=0時刻產生的粒子,恰好在t=2T0時刻從B板中心的小孔Q處穿過,并在t=3T0時刻緊貼D板的右邊緣離開,求:查看答案和解析>>
科目:高中物理 來源: 題型:計算題
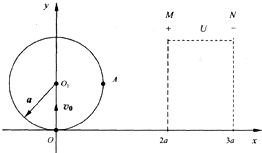 如圖所示,在坐標系xOy內有一半徑為d的圓形區域,圓心坐標為O1(0,a),圓內分布有垂直紙面向里的勻強磁場.在M、N之間的矩形區域(即x=2a,x=3a和y=0,y=2a所圍成的區域)內有一沿+x方向的勻強電場.一質量為m、電荷量為-q(q>0)的粒子以速度v0從O點垂直于磁場沿+y軸方向射入,粒子恰好從A點射出磁場,A、O1兩點的連線與x軸平行.(不計粒子重力)
如圖所示,在坐標系xOy內有一半徑為d的圓形區域,圓心坐標為O1(0,a),圓內分布有垂直紙面向里的勻強磁場.在M、N之間的矩形區域(即x=2a,x=3a和y=0,y=2a所圍成的區域)內有一沿+x方向的勻強電場.一質量為m、電荷量為-q(q>0)的粒子以速度v0從O點垂直于磁場沿+y軸方向射入,粒子恰好從A點射出磁場,A、O1兩點的連線與x軸平行.(不計粒子重力)查看答案和解析>>
科目:高中物理 來源: 題型:選擇題
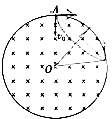 如圖所示,在半徑為R的圓形區域內有一磁感應強度方向垂直于紙面向里的勻強磁場,一質量為m且帶正電的粒子(重力不計)以初速度v0從圓形邊界上A點正對圓心射入該磁場區域,若該帶電粒子在磁場中運動的軌跡半徑為$\sqrt{3}$R,則下列說法中正確的是( )
如圖所示,在半徑為R的圓形區域內有一磁感應強度方向垂直于紙面向里的勻強磁場,一質量為m且帶正電的粒子(重力不計)以初速度v0從圓形邊界上A點正對圓心射入該磁場區域,若該帶電粒子在磁場中運動的軌跡半徑為$\sqrt{3}$R,則下列說法中正確的是( )| A. | 該帶電粒子在磁場中將向左偏轉 | |
| B. | 該帶電粒子在磁場中運動的時間為$\frac{\sqrt{3}πR}{3{v}_{0}}$ | |
| C. | 該帶粒子的軌跡圓弧對應的圓心角為30° | |
| D. | 若增大磁場的磁感應強度,則該帶電粒子在磁場中運動的軌道半徑將變大 |
查看答案和解析>>
科目:高中物理 來源: 題型:填空題
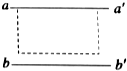 如圖所示,某同學在利用插針法測定玻璃磚折射率的實驗中誤將界面bb′畫得離開玻璃磚邊緣一段距離,但自己并未察覺.則他測得的折射率將小于(填“大于”、“等于”或“小于”真實值).
如圖所示,某同學在利用插針法測定玻璃磚折射率的實驗中誤將界面bb′畫得離開玻璃磚邊緣一段距離,但自己并未察覺.則他測得的折射率將小于(填“大于”、“等于”或“小于”真實值).查看答案和解析>>
科目:高中物理 來源: 題型:計算題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com